Tam giác vuông là một trong những hình học cơ bản trong toán học. Việc chứng minh đường cao trong tam giác vuông là một bài toán thường được giới thiệu đầu tiên trong chương trình học Toán ở trường học. Tuy nhiên, việc chứng minh đường cao này có thể không đơn giản cho những người mới bắt đầu học Toán. Trong bài viết này, chúng ta sẽ cùng Dapanchuan.com tìm hiểu cách chứng minh đường cao trong tam giác vuông một cách dễ hiểu và chi tiết nhất.
Đường cao trong tam giác vuông là gì?
Đường cao trong tam giác vuông là đoạn thẳng kết nối đỉnh vuông của tam giác với đường thẳng chứa cạnh đối vuông và vuông góc với cạnh đó. Đường cao này cũng là đường trung bình và đường trực tâm của tam giác vuông đó. Trong tam giác vuông, đường cao từ đỉnh vuông đồng thời là cạnh huyền của tam giác vuông đó.
Tính chất của đường cao trong tam giác vuông
Tam giác vuông là loại tam giác đặc biệt có một góc vuông. Điều này khiến cho đường cao tam giác vuông có một số tính chất khác biệt. Những tính chất này rất hữu ích trong quá trình làm bài tập và ứng dụng trong cuộc sống. Dưới đây là các tính chất cần nhớ về đường cao trong tam giác vuông:
- Tính chất thứ nhất: Trong tam giác vuông, tích của đường cao với cạnh huyền tương ứng bằng tích của hai cạnh góc vuông trong tam giác.
- Tính chất thứ hai: Trong tam giác vuông, bình phương của cạnh góc vuông bằng cạnh huyền nhân đường cao tương ứng chiếu trên cạnh huyền.
- Tính chất thứ ba: Trong tam giác vuông, bình phương của đường cao trên cạnh huyền bằng tích của hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
- Tính chất thứ tư: Trong tam giác vuông, nghịch đảo của bình phương mỗi cạnh góc vuông bằng nghịch đảo của bình phương đường cao.
Công thức tính đường cao trong tam giác vuông
Dựa vào công thức tính cạnh cùng đường cao trong tam giác vuông, ta có công thức tính đường cao trong dạng tam giác vuông như sau:
- a² = b² – c²
- b² = a.b′ và c²= a.c′
- a.h= b.c
- h²= b′.c′
- 1/b²=1/b²+1/c²
Trong đó:
- a, b, c: độ dài các cạnh thuộc tam giác vuông.
- b’: đường chiếu của cạnh b tương ứng trên cạnh huyền.
- c’: đường chiếu của cạnh c tương ứng trên cạnh huyền.
- h: đường cao hạ xuống từ đỉnh góc vuông.
Cách chứng minh đường cao trong tam giác vuông
Để chứng minh rằng đường cao trong tam giác vuông là đoạn thẳng kết nối đỉnh vuông của tam giác với đường thẳng chứa cạnh đối vuông và vuông góc với cạnh đó, ta có thể làm như sau:
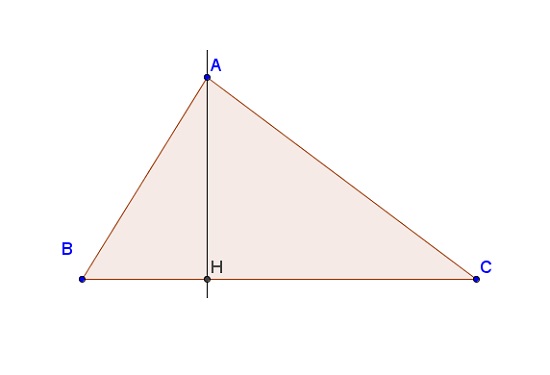
Giả sử tam giác ABC là tam giác vuông tại A, với cạnh huyền BC. Kẻ đường cao AH kẻ từ đỉnh A xuống cạnh huyền BC.
Ta cần chứng minh rằng đường cao AH là đường thẳng kết nối đỉnh vuông A với đường thẳng chứa cạnh đối vuông BC và vuông góc với cạnh đó.
Ta cần chứng minh rằng hai tam giác AHB và AHC đều vuông.
- Tam giác AHB vuông tại H: Vì AH là đường cao của tam giác ABC, nên AH vuông góc với BC tại H. Vì ABC là tam giác vuông tại A, nên AB là cạnh đối vuông với BC. Từ đó suy ra AB vuông góc với BC tại B. Vậy ta có hai đường thẳng AH và AB đều vuông góc với cạnh BC, nên tam giác AHB là tam giác vuông tại H.
- Tam giác AHC vuông tại H: Tương tự, ta có AC vuông góc với BC tại C. Vì AH vuông góc với BC tại H, nên ta có hai đường thẳng AH và AC đều vuông góc với cạnh BC, suy ra tam giác AHC cũng vuông tại H.
Do đó, ta chứng minh được rằng đường cao AH chính là đường thẳng kết nối đỉnh vuông A với đường thẳng chứa cạnh đối vuông BC và vuông góc với cạnh đó.
Bài tập vận dụng về đường cao trong tam giác vuông
1. Cho tam giác ABC vuông tại A có đường cao AH (H ∊ BC), biết rằng BH= 9m và BC= 25m. Tính độ dài đường cao trong tam giác ABC?
Lời giải tham khảo:
H ∊ BC mà BH= 9m, BC= 25m
⇒ CH= 25 – 9 = 16 (m)
Áp dụng công thức tính cạnh cùng đường cao trong tam giác vuông, ta có:
*) AH² = BH x CH = 9 x 16 = 144
⇒ AH = 12 (m)
*) AB² = BC x BH = 25 x 9 = 225
⇒ AB = 15 (m)
*) AC² = BC x CH = 25 x 16 = 400
⇒ AC = 20 (m)
Vậy độ dài đường cao trong △ABC vuông tại A là AH = 12m.
2. Cho tam giác ABC có góc vuông tại A, biết rằng AB=24cm, AC=32cm. Đường trung trực của đường thẳng BC sẽ cắt AC, BC theo thứ tự lần lượt là D, E. Tính DE.
Giải:
Xét trong phạm vi tam giác vuông ABC, ta có:
BC^2 = AB^2+ AC^2 ( theo định lý py-ta-go)
BC^2 = 24^2+ 32^2
BC2 = 1600
BC = 40(cm)
EC = BC : 2 = 40 : 2 = 20(cm)
– Xét theo tam giác vuông ACB, tam giác vuông ECD. Ta có góc A = góc E = 90o và góc C chung.
=> Tam giác ACB ∾ tam giác ECD
=> AC/EC = AB/ED
=> ED = AB.EC/AC = 15cm
Vậy ED = 15cm.
Tổng kết lại, việc chứng minh đường cao trong tam giác vuông có thể đơn giản nhưng cũng có thể phức tạp đối với những người mới bắt đầu học Toán. Tuy nhiên, nếu bạn hiểu rõ các bước chứng minh và áp dụng chúng một cách chính xác, việc chứng minh đường cao sẽ không còn là một thách thức đối với bạn. Hy vọng bài viết này đã giúp bạn cải thiện kỹ năng Toán của mình.