Tam giác đều là một trong những hình học cơ bản và quen thuộc nhất trong toán học. Với những tính chất đặc biệt của nó, tam giác đều có thể giúp chúng ta giải quyết nhiều bài toán phức tạp. Trong bài viết này của Dapanchuan.com, chúng ta sẽ tìm hiểu về tính chất và cách tính đường cao của tam giác đều. Bài toán này không chỉ có ý nghĩa trong giáo dục mà còn ứng dụng rất nhiều trong thực tế, từ kiến trúc đến các ngành kỹ thuật.
Định nghĩa đường cao của tam giác đều
Tam giác đều là gì?
Tam giác đều có đường cao bằng đường trung bình và đường trung trực của đường chéo. Trong hình học, tam giác đều là một tam giác có ba cạnh bằng nhau hoặc ba góc bằng nhau, và mỗi góc bằng 60 độ. Nó còn được gọi là đa giác đều với số cạnh bằng ba.
Đường cao của tam giác đều là gì?
Đường cao trong tam giác đều là đường thẳng được kẻ từ một đỉnh đến cạnh đối diện và có độ dài bằng độ dài của đường thẳng đó. Đường cao trong tam giác đều cũng là đường trung trực của cạnh đối diện và đường phân giác của góc tại đỉnh tam giác, đồng thời cũng là đường trung tuyến trong tam giác.
Nó cũng chia góc ở đỉnh thành hai góc có cùng số độ và chia tam giác đều thành hai tam giác vuông bằng nhau. Mỗi tam giác có ba đường cao.
Tính chất đường cao của tam giác đều
Tam giác đều là tam giác có ba cạnh bằng nhau và các góc bằng nhau 60 độ. Điều này đồng nghĩa với việc các đường cao trong tam giác đều có cùng độ dài. Ngoài ra, đường cao trong tam giác đều còn có những tính chất đặc biệt như sau:
- Tam giác đều có ba đường cao, mỗi đường cao xuất phát từ một đỉnh và vuông góc với cạnh đối diện.
- Đường cao trong tam giác đều chia đôi góc ở đỉnh và tạo thành hai góc bằng nhau có độ lớn 30 độ.
- Đường cao trong tam giác đều đồng thời là đường trung trực, đường phân giác và đường trung tuyến.
- Đường cao trong tam giác đều còn chia cạnh đáy thành hai phần bằng nhau và mỗi đường cao sẽ chia tam giác đó thành hai tam giác bằng nhau có diện tích như nhau.
Công thức tính diện tích và chu vi của tam giác đều
Trước khi tìm hiểu công thức tính đường cao của tam giác đều thì chúng ta cùng tìm hiểu qua công thức tính diện tích và chu vi tam giác đều như sau:
– Diện tích tam giác đều: Diện tích tam giác đều bằng 1/2 tích của đáy nhân với chiều cao, công thức như sau:
S = 1/2 (a x h)
Trong đó:
- S là diện tích của tam giác
- a là chiều dài của cạnh cơ sở
- h là chiều cao
– Chu vi tam giác đều: Chu vi hình tam giác đều bằng tổng 3 cạnh của tam giác, công thức:
P = 3a
Trong đó:
- P là chu vi của tam giác
- a là cạnh của tam giác
– Bán kính đường tròn nội tiếp tam giác đều: r = a x √3 / 6
– Bán kính đường tròn ngoại tiếp tam giác đều: R = a x √3 / 3
– Ví dụ: Tính diện tích và chu vi tam giác đều cạnh:
a, Độ dài một cạnh của tam giác là 6cm.
b, Độ dài một cạnh của tam giác là 4cm.
c, Độ dài một cạnh của tam giác là 8cm.
Câu trả lời:
a, Diện tích của tam giác là: (6 x 6 x √3) / 4 = 9√3 (cm2)
Chu vi của tam giác là: 18cm
b, Diện tích hình tam giác là: (4 x 4 x √3) / 4 = 4√3 (cm2)
Chu vi của tam giác là: 12cm
c, Diện tích của tam giác là: (8 x 8 x √3) / 4 = 16√3 (cm2)
Chu vi của tam giác là: 24cm
– Một số lưu ý khi tính diện tích tam giác:
- Nếu tam giác có góc bẹt, chiều cao của nó nằm bên ngoài tam giác, khi đó cạnh để tính diện tích sẽ là cạnh trong tam giác.
- Khi tính diện tích tam giác, cần xác định rõ chiều cao ứng với đáy đó.
- Nếu hai tam giác có chung chiều cao hoặc chiều cao bằng nhau, thì diện tích hai tam giác sẽ tỉ lệ với 2 cạnh đáy. Ngược lại, nếu hai tam giác có chung đáy (hoặc hai đáy bằng nhau), diện tích tam giác tỉ lệ với 2 đường cao tương ứng.
Cách tính đường cao của tam giác đều
– Để tính đường cao trong dạng tam giác đều ABC có độ dài bằng a. Đường cao kẻ từ đỉnh A đến cạnh đáy BC là AH sẽ có độ dài là h, ta sẽ tính như sau:
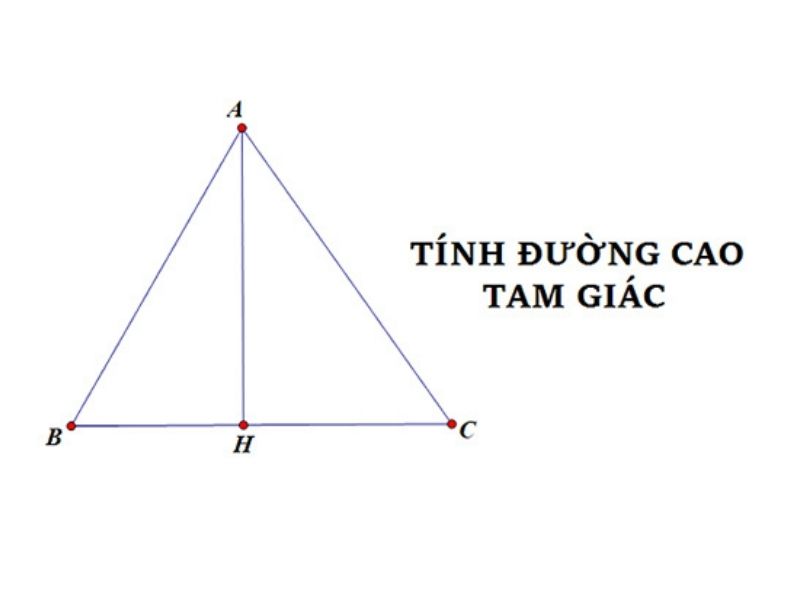
+ Vì tam giác ABC là dạng tam giác đều nên cả 3 cạnh của tam giác đều bằng a.
+ Theo tính chất của dạng tam giác đều thì đường cao AH chính là đường trung tuyến. Vì vậy nên đường cao AH sẽ phân chia cạnh đáy BC thành hai phần bằng nhau: BH = HC = a/2.
+ Để tính được độ dài của đường cao AH, chúng ta áp dụng định lý Pitago trong tam giác vuông ABH, ta có:
AB^2 = AH^2 + BH^2
<=> AH^2 = AB^2 – BH^2
Thay giá trị vào ta có:
h^2 = a^2 – (a/2)^2 = a2 – (a^2)/4 = (3a^2)/4
=> h = (a√3)/2
+ Kết luận: Đường cao trong tam giác đều có cạnh = a thì sẽ có độ dài bằng a√3/2 (đvđ).
Bài tập vận dụng tính đường cao của tam giác đều
Bài tập 1: Tính độ dài đường cao của tam giác đều có chu vi là 18 cm.
Giải:
Ta biết rằng chu vi của tam giác đều là:
C = 3a
với a là độ dài của mỗi cạnh của tam giác.
Do đó, ta có:
a = C/3 = 18/3 = 6 cm
Để tính độ dài đường cao của tam giác đều, ta áp dụng công thức:
AH = (a√3)/2
Vậy độ dài đường cao của tam giác đều này là:
AH = (6√3)/2 = 3√3 cm
Đáp số: 3√3 cm
Bài tập 2: Tính độ dài đường cao của tam giác đều có cạnh bằng 12 cm.
Giải:
Ta biết rằng độ dài đường cao của tam giác đều là:
AH = (a√3)/2
với a là độ dài của mỗi cạnh của tam giác.
Do đó, ta có:
AH = (12√3)/2 = 6√3 cm
Đáp số: 6√3 cm
Bài tập 3: Tính độ dài đường cao của tam giác đều có chu vi là 30√3 cm.
Giải:
Ta biết rằng chu vi của tam giác đều là:
C = 3a
với a là độ dài của mỗi cạnh của tam giác.
Do đó, ta có:
a = C/3 = (30√3)/3 = 10√3
Để tính độ dài đường cao của tam giác đều, ta áp dụng công thức:
AH = (a√3)/2
Vậy độ dài đường cao của tam giác đều này là:
AH = (10√3 * √3)/2 = 15 cm
Đáp số: 15 cm
Tổng kết lại, trong bài viết này, chúng ta đã tìm hiểu rõ về tính chất và cách tính đường cao của tam giác đều. Đường cao là một khái niệm quan trọng trong toán học và được áp dụng rộng rãi trong các lĩnh vực khác nhau. Việc hiểu và áp dụng đúng công thức tính đường cao sẽ giúp chúng ta giải quyết các bài toán liên quan đến tam giác đều một cách dễ dàng và chính xác.