Trong hình học, để viết phương trình đường trung tuyến, ta cần xác định được đỉnh của tam giác và trung điểm của cạnh đối diện. Sau đó, ta áp dụng định nghĩa đường trung tuyến để viết phương trình đường thẳng đi qua hai điểm đó. Vậy hãy cùng DapAnChuan.Com tìm hiểu ngay bên dưới về cách viết phương trình đường trung tuyến cụ thể.
Đường trung tuyến trong tam giác là gì?
Đường trung tuyến trong tam giác là đường thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện đỉnh đó. Mỗi tam giác có ba đường trung tuyến, mỗi đường trung tuyến bắt đầu từ một đỉnh và kết thúc tại trung điểm của cạnh đối diện đỉnh đó.
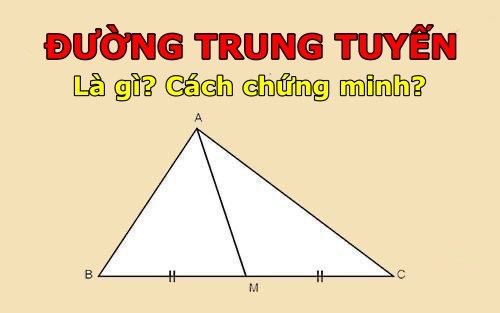
Đặc điểm quan trọng của đường trung tuyến là chúng luôn cắt nhau tại một điểm, được gọi là trọng tâm của tam giác. Trọng tâm là giao điểm của ba đường trung tuyến và nằm ở bên trong tam giác. Điểm này được ký hiệu là G và được coi là trọng lực tập trung của tam giác.
Tìm phương trình đường trung tuyến bằng cách nào?
Để tìm phương trình đường trung tuyến của một tam giác, ta có thể sử dụng một trong hai cách sau:
Cách 1: Sử dụng tọa độ của hai điểm đầu và cuối của đường trung tuyến
Đường trung tuyến của một tam giác là đường thẳng đi qua trung điểm của một cạnh và điểm đối diện với cạnh đó. Do đó, để tìm phương trình đường trung tuyến, ta cần tìm tọa độ của hai điểm này.
Tọa độ của trung điểm của một cạnh được tính như sau:
- (x1 + x2)/2, (y1 + y2)/2
- với (x1, y1) và (x2, y2) là tọa độ của hai điểm đầu và cuối của cạnh đó.
Tọa độ của điểm đối diện với cạnh đó được tính như sau:
- (x1 + x2)/2, (y1 + y2)/2
- với (x1, y1) là tọa độ của đỉnh của tam giác và (x2, y2) là tọa độ của trung điểm của cạnh đối diện với đỉnh đó.
Sau khi có tọa độ của hai điểm đầu và cuối của đường trung tuyến, ta có thể sử dụng công thức tính phương trình đường thẳng để tìm phương trình của đường trung tuyến đó.
Cách 2: Sử dụng tính chất của đường trung tuyến
Đường trung tuyến của một tam giác chia cạnh đối diện thành hai đoạn có độ dài bằng nhau. Do đó, ta có thể sử dụng tính chất này để tìm phương trình đường trung tuyến.
- Cho tam giác ABC với đường trung tuyến AM.
- Gọi D và E là trung điểm của AB và AC.
Theo tính chất của đường trung tuyến, ta có DE = BC/2.
Ta có thể sử dụng công thức tính phương trình đường thẳng đi qua hai điểm để tìm phương trình của đường trung tuyến AM.
- y – y1 = (y2 – y1)/(x2 – x1)*(x – x1)
- với (x1, y1) là tọa độ của điểm A, (x2, y2) là tọa độ của điểm D.
Cách viết phương trình đường trung tuyến
Có hai cách viết phương trình đường trung tuyến của tam giác:
Cách 1: Sử dụng định nghĩa đường trung tuyến
Đường trung tuyến của tam giác là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Do đó, ta có thể viết phương trình đường trung tuyến bằng cách cho tọa độ của đỉnh và trung điểm của cạnh đối diện.
Ví dụ: Cho tam giác ABC có đỉnh A có tọa độ (a, b), trung điểm của cạnh BC có tọa độ (x, y). Khi đó, đường trung tuyến ứng với cạnh BC có phương trình là:
- y – b = (y – x)/(2) * (x – a)
Cách 2: Sử dụng tính chất của đường trung tuyến
Đường trung tuyến của tam giác chia tam giác thành hai tam giác có diện tích bằng nhau. Do đó, ta có thể sử dụng tính chất này để viết phương trình đường trung tuyến.
Ví dụ: Cho tam giác ABC có đỉnh A có tọa độ (a, b), trung điểm của cạnh BC có tọa độ (x, y). Khi đó, ta có thể viết phương trình đường trung tuyến ứng với cạnh BC như sau:
- y – b = 2 * (y – x) / (x – a) * (x – a)
Cả hai cách viết trên đều cho ra kết quả chính xác. Cách viết thứ nhất đơn giản hơn, trong khi cách viết thứ hai sử dụng tính chất của đường trung tuyến, do đó có thể áp dụng cho các trường hợp tam giác đặc biệt.
Viết phương trình tổng quát của đường trung tuyến
Phương trình tổng quát của đường trung tuyến của tam giác là:
- y – y_m = k(x – x_m)
Trong đó:
ym và xm là tọa độ của trung điểm cạnh đối diện với đỉnh mà đường trung tuyến đi qua.
k là hệ số góc của đường trung tuyến.
Để tìm hệ số góc k, ta sử dụng công thức:
- k = (y_2 – y_1)/(x_2 – x_1)
Trong đó:
- y1 và x1 là tọa độ của đỉnh mà đường trung tuyến đi qua.
- y2 và x2 là tọa độ của trung điểm cạnh đối diện với đỉnh đó.
Ví dụ: Cho tam giác ABC với đỉnh A có tọa độ (1,1), đỉnh B có tọa độ (2,2) và đỉnh C có tọa độ (3,3). Trung điểm của cạnh BC có tọa độ (2.5,2.5).
Tọa độ của trung điểm cạnh BC là:
- (x_m, y_m) = (2.5, 2.5)
Hệ số góc của đường trung tuyến AM là:
- k = (y_2 – y_1)/(x_2 – x_1) = (2.5 – 1)/(3 – 1) = 1.5
Vậy phương trình đường trung tuyến AM là:
- y – 2.5 = 1.5(x – 2.5)
Hoặc:
- y – 2.5 = 1.5x – 3.75
- y = 1.5x + 1
Phương trình này có dạng y = kx + b, trong đó k = 1.5 và b = 1.
Chú ý: Đường trung tuyến của tam giác luôn đi qua trọng tâm của tam giác.
Các dạng bài tập viết phương trình đường trung tuyến
Cho biết đỉnh và trung điểm của cạnh đối diện
Phương pháp giải: Xác định tọa độ của đỉnh và trung điểm của cạnh đối diện.
Sử dụng công thức tính đường trung tuyến:
- d = 2s/3
Trong đó:
- d là độ dài đường trung tuyến
- s là nửa chu vi tam giác
Viết phương trình đường trung tuyến theo tọa độ của đỉnh và trung điểm của cạnh đối diện.
Cho biết 2 đỉnh của tam giác
Phương pháp giải: Xác định tọa độ của 2 đỉnh của tam giác.
Sử dụng công thức tính trung điểm của cạnh:
(x1 + x2)/2, (y1 + y2)/2
Trong đó:
- (x1, y1) là tọa độ của đỉnh thứ nhất
- (x2, y2) là tọa độ của đỉnh thứ hai
Sử dụng công thức tính đường trung tuyến:
- d = 2s/3
Trong đó:
- d là độ dài đường trung tuyến
- s là nửa chu vi tam giác
Viết phương trình đường trung tuyến theo tọa độ của trung điểm của cạnh đối diện.
Viết phương trình đường trung tuyến AM
Cho tam giác ABC có đỉnh A(1, 2), B(3, 4), C(5, 6). Viết phương trình đường trung tuyến AM theo tọa độ đỉnh và trung điểm
Tọa độ của trung điểm M của cạnh BC là:
- M = (3 + 5)/2, (4 + 6)/2 = 4, 5
Vậy phương trình đường trung tuyến AM là:
- (x – 1)/(4 – 1) = (y – 2)/(5 – 2) = (z – 3)/(6 – 3)
- x – 1 = y – 2
- y = x + 1

Vậy phương trình đường trung tuyến AM là:
- y = x + 1
Phương trình đường trung tuyến AM theo véc-tơ chỉ phương
Véc-tơ chỉ phương của đường trung tuyến AM là:
- (5 – 1, 6 – 2, 6 – 3)/2 = 2, 2, 1
Vậy phương trình đường trung tuyến AM là:
- 2x + 2y + z = 0
Kết luận
- Phương trình đường trung tuyến AM có thể được viết theo tọa độ đỉnh và trung điểm hoặc véc-tơ chỉ phương.
Viết phương trình đường trung tuyến BM
Đường trung tuyến BM là đường thẳng đi qua trung điểm của cạnh BC và đỉnh B của tam giác ABC.
Gọi M là trung điểm của cạnh BC, ta có:
Tọa độ điểm M:
- M = (x_c + x_b)/2, (y_c + y_b)/2
Tọa độ điểm B:
- B = (x_b, y_b)
Vậy phương trình đường trung tuyến BM có dạng:
- y – y_b = (y_c – y_b)/(x_c – x_b) * (x – x_b)
Cách giải:
Bước 1: Tìm tọa độ điểm M.
Ta có:
M = (x_c + x_b)/2, (y_c + y_b)/2
Bước 2: Tìm hệ số góc của đường trung tuyến.
Hệ số góc của đường trung tuyến BM là:
k = (y_c – y_b)/(x_c – x_b)
Bước 3: Viết phương trình đường trung tuyến BM.
Ta có:
y – y_b = k * (x – x_b)
Ví dụ:
Cho tam giác ABC có đỉnh A (2, 3), B (-1, 1) và C (4, 5). Tìm phương trình đường trung tuyến BM.
Bước 1: Tìm tọa độ điểm M.
M = (x_c + x_b)/2, (y_c + y_b)/2
M = ((-1) + 4)/2, ((1) + 5)/2
M = (1.5, 3)
Bước 2: Tìm hệ số góc của đường trung tuyến.
k = (y_c – y_b)/(x_c – x_b)
k = (5 – 1)/(4 – (-1)) = 4/5
Bước 3: Viết phương trình đường trung tuyến BM.
y – 3 = 4/5 * (x – 1.5)
5y – 15 = 4x – 6
5y – 4x = -9
Vậy phương trình đường trung tuyến BM là 5y – 4x = -9.
Kết luận:
Phương trình đường trung tuyến BM có dạng:
- y – y_b = k * (x – x_b)
với:
- M là trung điểm của cạnh BC.
- k là hệ số góc của đường trung tuyến.
Tọa độ điểm M và hệ số góc k có thể được tìm theo các bước sau:
Bước 1: Tìm tọa độ điểm M.
M = (x_c + x_b)/2, (y_c + y_b)/2
Bước 2: Tìm hệ số góc của đường trung tuyến.
k = (y_c – y_b)/(x_c – x_b)
Viết phương trình đường trung tuyến CM
Đường trung tuyến CM đi qua đỉnh C và trung điểm M của cạnh AB.
Tọa độ trung điểm M của đoạn thẳng AB là:
- M = (xA + xB)/2, (yA + yB)/2
Thay tọa độ điểm C và M vào phương trình đường thẳng ta được:
y – yC = (yM – yC)/(xM – xC)(x – xC)
y – yC = (yM – yC)/(2x – 2xC)(x – xC)
y – yC = (yM – yC)/(2(x – xC))
2(y – yC) = (yM – yC)(x – xC)
2y – 2yC = (yM – yC)(x – xC)
2y = (yM – yC)(x – xC) + 2yC
2y = (yB – yA)(x – xA) + 2yC
Vậy phương trình đường trung tuyến CM là:
- y = (yB – yA)(x – xA)/2 + yC
Ví dụ: Cho tam giác ABC có tọa độ đỉnh A là (1, 2), đỉnh B là (3, 4) và đỉnh C là (5, 6).
Tọa độ trung điểm M của cạnh AB là:
M = (1 + 3)/2, (2 + 4)/2 = (2, 3)
Thay tọa độ điểm C và M vào phương trình đường trung tuyến ta được:
y = (6 – 2)(x – 1)/2 + 6 = (4)(x – 1) + 6 = 4x – 2 + 6 = 4x + 4
Vậy phương trình đường trung tuyến CM là:
y = 4x + 4
Đường trung tuyến CM đi qua điểm C (5, 6) và có phương trình y = 4x + 4.
Phương trình đường trung tuyến trong không gian trục OXYZ
Đường trung tuyến trong không gian là đường thẳng đi qua một đỉnh của tam giác và trung điểm của cạnh đối diện. Đường trung tuyến của tam giác chia tam giác thành hai tam giác có diện tích bằng nhau.
Phương trình đường trung tuyến trong không gian được viết như sau:
ax + by + c = 0
Trong đó:
- (a, b, c) là véc-tơ chỉ phương của đường thẳng
- M là trung điểm của cạnh đối diện với đỉnh A
- P là điểm bất kỳ trên đường trung tuyến
Cách tìm véc-tơ chỉ phương của đường trung tuyến
Để tìm véc-tơ chỉ phương của đường trung tuyến, ta có thể sử dụng công thức sau:
(x2 – x1, y2 – y1, z2 – z1)/2
trong đó:
- (x1, y1, z1) là tọa độ của đỉnh A
- (x2, y2, z2) là tọa độ của điểm M
Cách viết phương trình đường trung tuyến theo tọa độ đỉnh và trung điểm
Ta có thể viết phương trình đường trung tuyến theo tọa độ đỉnh và trung điểm của cạnh đối diện như sau:
(x – x1)/(x2 – x1) = (y – y1)/(y2 – y1) = (z – z1)/(z2 – z1)
Trong đó:
- (x1, y1, z1) là tọa độ của đỉnh A
- (x2, y2, z2) là tọa độ của điểm M
Hy vọng mọi người sẽ hiểu rõ hơn về các thông tin về cách viết phương trình đường trung tuyến trong bài viết trên. Phương trình đường trung tuyến có nhiều ứng dụng trong thực tế, chẳng hạn như trong việc tính toán diện tích và thể tích của tam giác, trong việc xác định trọng tâm của tam giác,…vv. Mong rằng những kiến thức trên sẽ giúp ích cho các bạn trong quá trình học tập và nghiên cứu.