Tam giác cân là gì, định nghĩa, tính chất của tam giác cân ? đây là câu hỏi được các bạn học sinh thắc mắc nhiều nhất trong thời gian qua. Vì thế mà với chủ đề lần này Dapanchuan.com xin gởi đến các bạn một số những thông tin hữu ích liên quan về Tam giác cân.

Vậy Tam giác cân là gì? định nghĩa về tam giác cân?
Hình tam giác là một hình học cơ bản trong môn toán Hình. Tam giác là hình có đa giác lồi và có ba cạnh nối ba điểm không thẳng hàng lại với nhau tạo thành ba đỉnh của tam giác.
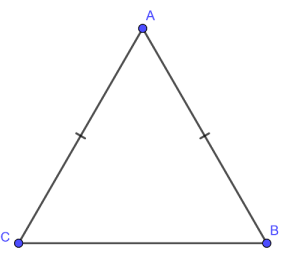
Khi bắt gặp một hình Tam giác mà ở đó có hai cạnh của tam giác đó bằng nhau thì được gọi là tam giác cân. Hai cạnh này được gọi là hai cạnh bên và cạnh còn là cạnh đáy.
Giao điểm của hai cạnh bên tạo thành góc ở đỉnh của tam giác. Và giao của cạnh đáy với hai cạnh bên tạo thành hai góc ở đáy.
Tính chất của tam giác cân:
Tam giác cân là tam giác có hai góc ở đáy bằng nhau
Nếu bắt gặp một tam giác nào đó có 2 cạnh bằng nhau thì tam giác đó được gọi là tam giác cân.
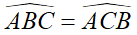

Cách tính chu vi tam giác cân
Để tính chu vi tam giác cân, bạn cần biết đỉnh của tam giác cân và độ dài 2 cạnh là được. Công thức tính chu vi hình tam giác cân là:
P = 2a + c
Trong đó:
a: Hai cạnh bên của tam giác cân.
c: Là đáy của tam giác.
Lưu ý, công thức tính chu vi tam giác cân sẽ được áp dụng để tính chu vi của tam giác vuông cân.
Ví dụ: Cho hình tam giác cân tại A với chiều dài AB = 7cm, BC = 5cm. Tính chu vi hình tam giác cân.
Dựa vào công thức tính chu vi tam giác cân, ta có cách tính P = 7 + 7 + 5 = 19cm.
Công thức tính diện tích tam giác cân
Diện tích tam giác cân sẽ tính bằng bằng ½ tích đường cao hạ từ đỉnh nhân với cạnh đối diện của đỉnh đó.
S = ½ h x a
Trong đó:
S: Là diện tích.
h: Là đường cao.
a: Cạnh đối diện của đỉnh.
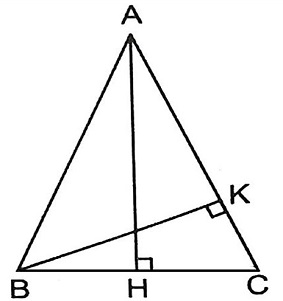
Ví dụ: Diện tích tam giác ABC trong hình vẽ được tính như sau:
Dựa vào công thức tính diện tích tam giác cân, ta có cách tính :
S = 1/2 BK x AC = 1/2 AH x BC.
Các dạng toán về tính chất tam giác cân
Với tam giác cân sẽ có rất nhiều bài tập liên quan đến nó và sau đây là những bài tập phổ biến nhất và thường gặp nhất mà Dapanchuan.com đã tổng hợp lại cho các bạn học sinh để các bạn phần nào có thể hình dung ra các dạng bài tập về tam giác cân một cách cụ thể nhất
Dạng 1: Bổ sung điều kiện để hai tam giác cân bằng nhau
Để giải được dạng toán này bạn cần dựa vào các trường hợp bằng nhau của hai tam giác kết hợp với định nghĩa, tính chất của tam giác cân.
Dạng 2: Sử dụng định nghĩa tam giác cân
Đây là dạng toán chứng minh bạn cần phải hiểu và nhớ được định nghĩa tam giác cân để áp dụng vào bài toán sao cho phù hợp.
Dạng 3: Sử dụng tính chất của tam giác cân
Đây là dạng bài phải sử dụng tính chất của tam giác cân để giải bài toán. Chính vì vậy, bạn cần phải hiểu rõ và ghi nhớ đủ các tính chất để làm dạng toán này nhé!
Một số lưu ý khi làm bài tập tam giác cân
Các bạn học sinh phải xác định rõ đây là tam gia cân gì? Việc nhớ rõ và xác định đúng tính chất của từng loại tam giác sẽ giúp các bạn học sinh dễ dàng hơn trong việc giải đề toán.
Dù là ở bất kỳ đề toán nào thì các bạn học sinh cũng cần phải thật cẩn thận mặc dù đó là một đề rất dễ. Đối với những bài toán có những phép tính phức tạp hoặc các con số có giá trị lớn thì các bạn học sinh nên sử dụng máy tính cầm tay để có được những đáp án chắc chắn.
Các đại lượng phải cùng đơn vị đo: Khi làm bài các bạn học sinh phải để ý yêu cầu ở đề bài xem các đại lượng tính toán có khác nhau hay không nếu khác thì bạn phải quy đổi về một đơn vị đo.
Hãy nhớ chính xác và áp dụng đúng công thức các bạn học sinh cần hiểu và nhớ tất cả các công thức tính diện tích, chu vi hay các công thức liên quan đến tam giác cân để khi gặp những dạng bài yêu cầu tính toán thì các bạn học sinh sẽ không rơi vào thế bị động.
Cách vẽ tam giác cân
Để có thể vẽ chuẩn một tam giác cân ta sẽ cần đến sự trợ giúp của compa. Ví dụ dưới đây sẽ giúp bạn hình dung rõ hơn cách sử dụng compa để vẽ tam giác cân.
Ví dụ: Vẽ tam giác ABC cân tại A.
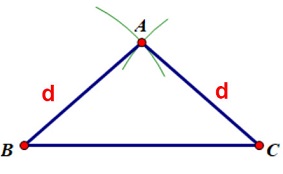
Bước 1: Hình dung, sắp xếp thứ tự của các cạnh và các góc.
Ta có: AB = AC là hai cạnh bên, BC sẽ là cạnh đáy. Góc BAC là góc ở đỉnh, góc ABC và góc ACB là góc ở đáy.
Bước 2: Vẽ tam giác cân
Sau khi thực hiện xong bước 1, bạn hãy sử dụng thước kẻ vẽ cạnh AC > Vẽ cung tròn tâm A bán kính d > Vẽ cung tròn tâm C bán kính d sao cho hai cung tròn cắt nhau. Giao điểm của hai cung tròn chính là đỉnh B.
Tam giác vuông cân
Tam giác vuông cân có góc bao nhiêu độ: Trong tam giác vuông cân có hai cạnh góc vuông bằng nhau và Hai góc ở đáy bằng nhau và bằng 45 độ.

Tam giác đều
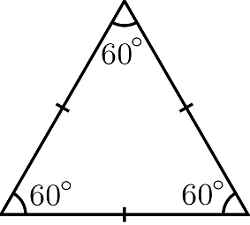
Tam giác đều:Tam giác đều là tam giác có ba cạnh bằng nhau. Nếu trong một tam giác có ba cạnh bằng nhau thì đó là tam giác đều.Nếu trong một tam giác có ba góc bằng nhau thì đó là tam giác đều. Nếu một tam giác cân có 1 góc bằng 60 độ thì đó là tam giác đều.

Cách tính chu vi tam giác đều
Tam giác đều là trường hợp đặc biệt của tam giác cân khi 3 cạnh bằng nhau. Công thức tính tam giác đều là:
P = 3 x a
Trong đó
P: Là chu vi tam giác đều.
a: Là chiều dài cạnh của tam giác.
Ví dụ: Tính chu vi tam giác đều có cạnh AB = 5cm.
Dựa theo công thức chúng ta có cách tính P = 5 x 3 = 15cm.