Trong toán hình học, đường cao của tam giác vuông là một tính chất quan trọng, có thể áp dụng để tính toán các thông số liên quan đến tam giác vuông một cách nhanh chóng và chính xác. Trong bài viết này, hãy cùng Đáp Án Chuẩn tập trung vào Giải Toán Chứng minh Cho Tam Giác ABC Vuông Tại A đường Cao AH ngay bên dưới
Xem: Công thức và Cách tính đường cao trong tam giác vuông cân
Định nghĩa tam giác vuông tại A
Một tam giác vuông tại A là một tam giác có một góc vuông tại đỉnh A. Nó có hai cạnh kề đỉnh A được gọi là các cạnh đối góc của nhau và độ dài bằng nhau, được ký hiệu là a. Hai cạnh còn lại của tam giác cũng có độ dài bằng nhau và được gọi là cạnh góc vuông của tam giác, thường được ký hiệu là b và c.
Tổng quát hơn, tam giác vuông tại A còn có thể được định nghĩa là tam giác có ba cạnh a, b và c, trong đó a là cạnh đối góc với góc vuông tại A và b, c là hai cạnh còn lại của tam giác.
Vị trí của đường cao trong tam giác ABC
Trong tam giác ABC, đường cao là đoạn thẳng kết nối một đỉnh của tam giác với đường thẳng chứa cạnh đối diện nó và vuông góc với cạnh đó. Tam giác có ba đường cao, mỗi đường cao kết nối một đỉnh với đường thẳng chứa cạnh đối diện nó.
Đường cao từ đỉnh A của tam giác ABC sẽ vuông góc với cạnh BC tại một điểm H nằm trên cạnh đó. Tương tự, đường cao từ đỉnh B sẽ vuông góc với cạnh AC tại một điểm K nằm trên cạnh đó, và đường cao từ đỉnh C sẽ vuông góc với cạnh AB tại một điểm L nằm trên cạnh đó.
Ba đường cao này đồng quy, có nghĩa là chúng đồng quy tại một điểm duy nhất, gọi là trung điểm Schiffler của tam giác ABC. Trung điểm Schiffler là trung điểm của đoạn thẳng nối trực tiếp giữa trung điểm hai cạnh của tam giác và trung điểm giữa hai điểm chính của tam giác.
Tính chất của đường cao trong tam giác vuông
Trong một tam giác vuông, đường cao là đoạn thẳng nối đỉnh vuông với đối diện cạnh của nó, vuông góc với cạnh đó. Dưới đây là một số tính chất của đường cao trong tam giác vuông:
- Trong một tam giác vuông, ba đường cao đều trùng nhau tại điểm giao nhau của chúng, được gọi là trung tuyến.
- Độ dài của đường cao có thể được tính bằng cách sử dụng định lý Pythagoras. Nếu gọi a, b, c lần lượt là độ dài của các cạnh của tam giác, và h là độ dài đường cao kẻ từ đỉnh vuông, ta có: h = c * sin(A) = b * sin(B) = a * sin(C), trong đó A, B, C lần lượt là các góc tại các đỉnh của tam giác vuông.
- Trong tam giác vuông, đường cao tương ứng với cạnh huyền của tam giác. Nó chia cạnh huyền thành hai đoạn thẳng bằng nhau, và chia diện tích tam giác làm hai phần bằng nhau.
- Đường cao cũng là đường trung bình của tam giác đó. Nghĩa là, nó chia đoạn thẳng nối đỉnh vuông với trung điểm của cạnh đối diện làm hai phần bằng nhau.
- Đường cao còn là đường phân giác của góc vuông. Nghĩa là, nó chia góc vuông thành hai góc bằng nhau.
Xem Hướng dẫn: cách tính chiều cao tam giác vuông
Công thức tính độ dài đường cao AH trong tam giác vuông
Trong tam giác vuông ABC tại đỉnh A, đường cao AH từ đỉnh A xuống đường BC là đường cao của tam giác đó. Để tính độ dài của đường cao AH, ta có thể sử dụng công thức sau đây:
Độ dài đường cao AH = p(AH) = p(BC) * sin(A)
Trong đó:
- p(AH) là độ dài của đường cao AH.
- p(BC) là độ dài của đoạn thẳng BC.
- A là góc tại đỉnh A (tức góc giữa đường cao AH và cạnh AB).
Chú ý rằng, trong tam giác vuông, góc tại đỉnh A là góc vuông (90 độ). Vì vậy, công thức trên có thể được viết lại như sau:
Độ dài đường cao AH = p(BC) * sin(90 độ) = p(BC)
Vì vậy, để tính độ dài của đường cao AH trong tam giác vuông tại đỉnh A, ta chỉ cần biết độ dài của đoạn thẳng BC (hoặc cạnh đối diện với đỉnh A).
Cho Tam Giác ABC Vuông Tại A đường Cao AH
Để giải bài tập về tam giác vuông tại A có đường cao AH, chúng ta cần biết rằng trong một tam giác vuông, đường cao từ đỉnh vuông góc đến cạnh huyền chính là đoạn thẳng trực diện với cạnh huyền chính.
Do đó, trong tam giác vuông tại A có đường cao AH, ta có thể biểu diễn AH là đường cao của tam giác, còn cạnh huyền chính là đoạn AB hoặc AC, tùy thuộc vào vị trí của đỉnh vuông góc.
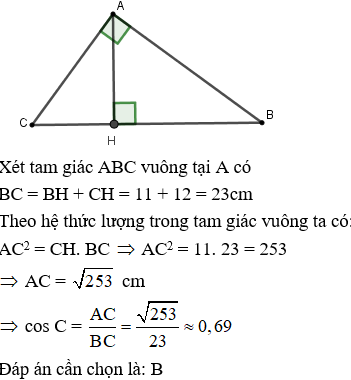
Để giải bài tập này, ta có thể sử dụng các định lý và công thức trong hình học Euclid, bao gồm định lý Pythagoras và các tỉ lệ trong tam giác đồng dạng.
Dưới đây là các bước giải chi tiết:
- Bước 1: Vẽ đường cao AH và đoạn AB hoặc AC tùy thuộc vào vị trí của đỉnh vuông góc.
- Bước 2: Sử dụng định lý Pythagoras để tính độ dài của các cạnh của tam giác. Cụ thể, nếu đỉnh vuông góc là A và cạnh huyền là AB, ta có:
AB^2 = AH^2 + HB^2
Trong đó, HB là độ dài của phần còn lại của cạnh AB sau khi loại bỏ đoạn AH.
- Bước 3: Giải phương trình để tìm độ dài của cạnh còn lại của tam giác. Trong trường hợp này, nếu ta biết độ dài cạnh AB và độ dài đường cao AH, ta có thể tìm được độ dài cạnh còn lại AC bằng cách sử dụng định lý Pythagoras như sau:
AC^2 = AB^2 – AH^2
- Bước 4: Tính diện tích của tam giác bằng công thức:
Diện tích tam giác = 1/2 x độ dài đường cao x độ dài cạnh gần đỉnh vuông góc.
Với tam giác vuông tại A có đường cao AH, diện tích tam giác có thể tính được bằng công thức:
Diện tích tam giác = 1/2 x AH x AB (nếu cạnh huyền là AB) hoặc Diện tích tam giác = 1/2 x AH x AC (nếu cạnh huyền là AC).
Hy vọng những giải thích trên có thể giúp bạn giải quyết bài tập về tam giác vuông tại A có đường cao AH.
Xem: Công thức tính diện tích tam giác vuông cân
Các dạng toán cho Tam Giác ABC Vuông Tại A đường Cao AH
Dưới đây là một số dạng bài tập liên quan đến đường cao AH trong tam giác ABC vuông tại đỉnh A:
- Tính độ dài đường cao AH khi biết chiều dài cạnh AB và cạnh AC của tam giác ABC.
Lời giải:
Để tính độ dài đường cao AH trong tam giác ABC, ta cần biết độ dài của cạnh đối diện với đỉnh A (hay còn gọi là cạnh BC).
Giả sử AB và AC lần lượt là độ dài của hai cạnh của tam giác ABC. Khi đó, ta có thể sử dụng định lý Pythagoras để tính độ dài của cạnh BC như sau:
BC² = AB² – AH²
Do đó, ta có thể tính độ dài của đường cao AH như sau:
AH = sqrt(AB² – BC²)
Với cách tính này, ta cần biết độ dài của cả hai cạnh AB và AC của tam giác ABC để tính được độ dài của đường cao AH.
- Tính diện tích tam giác ABC khi biết độ dài đường cao AH và độ dài cạnh AB hoặc cạnh AC.
Lời giải:
Nếu biết độ dài đường cao AH và độ dài cạnh AB, ta có thể tính diện tích tam giác ABC bằng công thức:
Diện tích tam giác ABC = (AB * AH) / 2
Nếu biết độ dài đường cao AH và độ dài cạnh AC, ta có thể tính diện tích tam giác ABC bằng công thức tương tự:
Diện tích tam giác ABC = (AC * AH) / 2
Trong cả hai công thức trên, đường cao AH là đường cao kẻ từ đỉnh A xuống cạnh BC, và độ dài cạnh AB hoặc AC là cạnh đối diện với đỉnh A tương ứng.
- Tính độ dài cạnh AB hoặc cạnh AC khi biết diện tích tam giác ABC và độ dài đường cao AH.
Lời giải:
Giả sử ta muốn tính độ dài cạnh AB. Để làm điều này, ta có thể sử dụng công thức tính diện tích của tam giác:
Diện tích tam giác ABC = (AB * AH) / 2
Từ đó, ta có thể giải phương trình trên để tìm độ dài cạnh AB:
AB = (2 * Diện tích tam giác ABC) / AH
Tương tự, nếu ta muốn tính độ dài cạnh AC, ta có thể sử dụng công thức:
AC = (2 * Diện tích tam giác ABC) / AK
trong đó AK là độ dài đường cao kẻ từ đỉnh A xuống cạnh BC
- Tính khoảng cách từ đỉnh A đến đường thẳng BC.
Lời giải:
Để tính khoảng cách từ đỉnh A đến đường thẳng BC trong tam giác ABC, ta có thể sử dụng công thức:
Khoảng cách từ đỉnh A đến đường thẳng BC = Diện tích tam giác ABC / độ dài cạnh BC
Trong đó, diện tích tam giác ABC có thể tính bằng công thức:
Diện tích tam giác ABC = (1/2) * AB * AH
trong đó AB là độ dài cạnh của tam giác ABC, và AH là độ dài đường cao từ đỉnh A xuống đường thẳng BC.
Độ dài cạnh BC có thể tìm bằng định lý Pythagoras:
BC^2 = AB^2 – AC^2
Do tam giác ABC là tam giác vuông tại A, nên:
BC = AB * sin(C)
Từ đó, ta có thể tính khoảng cách từ đỉnh A đến đường thẳng BC như sau:
Khoảng cách từ đỉnh A đến đường thẳng BC = (1/2) * AB * AH / (AB * sin(C)) = AH / 2 * sin(C)
Trong đó, C là góc tại đỉnh C của tam giác ABC.
- Tính diện tích tam giác ABH khi biết độ dài đường cao AH và độ dài cạnh AB.
Lời giải:
Để tính diện tích tam giác ABH khi biết độ dài đường cao AH và độ dài cạnh AB, ta sử dụng công thức:
Diện tích tam giác ABH = (1/2) * AB * AH
Trong đó AB là độ dài cạnh của tam giác ABC và AH là độ dài đường cao từ đỉnh A xuống cạnh BC, nhưng do tam giác ABH là tam giác vuông tại H nên cạnh đối diện với góc vuông là AH, và AB là cạnh kề.
Vì vậy, ta có thể sử dụng công thức trên để tính diện tích tam giác ABH khi biết độ dài AB và độ dài đường cao AH.
- Tìm tọa độ điểm H khi biết tọa độ của các đỉnh A, B, C.
Lời giải:
Để tìm tọa độ điểm H trong tam giác ABC, ta cần biết đường cao từ đỉnh A xuống đường thẳng BC. Để làm điều này, ta có thể sử dụng phương trình của đường thẳng BC và tính toán giao điểm giữa đường thẳng BC và đường thẳng vuông góc với BC và đi qua đỉnh A.
Giả sử tọa độ của đỉnh A là (x1, y1), tọa độ của đỉnh B là (x2, y2), và tọa độ của đỉnh C là (x3, y3). Khi đó, ta có thể tính độ dài đường thẳng BC bằng công thức khoảng cách Euclid:
BC = sqrt((x3 – x2)^2 + (y3 – y2)^2)
Tiếp theo, ta tính hệ số góc của đường thẳng BC:
m = (y3 – y2) / (x3 – x2)
Do đường thẳng vuông góc với BC và đi qua đỉnh A có hệ số góc là -1/m, nên ta có thể viết phương trình của đường thẳng vuông góc như sau:
y – y1 = (-1/m) * (x – x1)
Tương đương với:
y = (-1/m) * x + (y1 – (-1/m) * x1)
Sau đó, ta giải hệ phương trình gồm phương trình của đường thẳng BC và đường thẳng vuông góc qua đỉnh A để tính tọa độ của điểm H:
(xH, yH) = ((y1 – y2 + m * x2 – (1/m) * x1) / (2 * m), (y1 + y2 + m * x1 + (1/m) * x2) / 2)
Với tọa độ (xH, yH) là tọa độ của điểm H.
- Tìm tọa độ điểm H khi biết tọa độ của đỉnh A và phương trình đường thẳng BC.
Lời giải:
Để tìm tọa độ của điểm H trong tam giác ABC khi biết tọa độ của đỉnh A và phương trình đường thẳng BC, ta sử dụng phương pháp tính giao điểm giữa đường thẳng vuông góc với BC và đi qua A.
Đường thẳng vuông góc với BC và đi qua A sẽ có phương trình dạng:
y – yA = (-1/mBC) * (x – xA)
trong đó, (xA, yA) là tọa độ của đỉnh A, mBC là hệ số góc của đường thẳng BC. Hệ số góc mBC có thể được tính bằng cách lấy hiệu của hoành độ và tung độ của hai đỉnh B và C.
mBC = (yC – yB) / (xC – xB)
Sau đó, ta giải hệ phương trình gồm phương trình đường thẳng BC và phương trình đường thẳng vuông góc qua A để tìm tọa độ của điểm H. Điểm H chính là giao điểm giữa hai đường thẳng này.
Để giải hệ phương trình, ta cần chuyển đổi phương trình đường thẳng BC về dạng phương trình đường thẳng Ax + By + C = 0. Giả sử phương trình đường thẳng BC đã được cho dưới dạng này, ta có:
A_BC * x + B_BC * y + C_BC = 0
Trong đó, A_BC, B_BC và C_BC là các hệ số tương ứng của phương trình đường thẳng BC.
Tiếp theo, ta thay thế phương trình của y trong phương trình đường thẳng vuông góc qua A bằng (-1/mBC) * (x – xA) để có phương trình chỉ chứa biến x:
y – yA = (-1/mBC) * (x – xA)
y = (-1/mBC) * x + (yA – (-1/mBC) * xA)
Thay y bằng (-1/mBC) * x + (yA – (-1/mBC) * xA) vào phương trình đường thẳng BC, ta được:
A_BC * x + B_BC * ((-1/mBC) * x + (yA – (-1/mBC) * xA)) + C_BC = 0
Mở rộng và rút gọn biểu thức ta được:
x = (B_BC * yA – A_BC * B_BC * xA – C_BC * mBC) / (A_BC + B_BC * mBC)
Thay x vào phương trình đường thẳng vuông góc qua A để tính tọa độ y của điểm H:
y = (-1/mBC) * x + (yA – (-1/mBC) * xA)
Vậy tọa độ của điểm H là (x, y) = ((B_BC * yA – A_BC * B_BC * xA – C_BC * mBC) / (A_BC + B_BC * mBC), (-1/mBC) * ((B_BC * yA – A_BC * B_BC * xA – C_BC * mBC) / (A_BC + B_BC * mBC)) + (yA – (-1/mBC) * xA)).
Lưu ý: Nếu đường thẳng BC song song với trục tung, tức là mBC bằng vô cùng, thì không thể sử dụng phương pháp này để tính tọa độ của điểm H.
Ví dụ bài tập về tam giác vuông tại A đường cao AH
Cho tam giác vuông ABC tại đỉnh A, trong đó AB = 3 cm và AC = 4 cm. Tính độ dài của đường cao AH từ đỉnh A xuống đường BC.
Để giải bài toán này, ta cần tìm độ dài của cạnh đối diện với đỉnh A (hay còn gọi là cạnh BC) bằng cách sử dụng định lý Pythagoras:
- BC² = AC² – AB²
- BC² = 4² – 3²
- BC² = 7 BC = sqrt(7) ≈ 2.65 cm
Sau đó, ta có thể tính độ dài của đường cao AH từ đỉnh A xuống đường BC:
- AH = sqrt(AC² – BC²)
- AH = sqrt(4² – 7)
- AH = sqrt(9) AH = 3 cm
- Vậy, độ dài của đường cao AH là 3 cm.
Cho Tam Giác ABC Vuông Tại A đường Cao AH
Hy vọng rằng bài viết về nội dung Cho Tam Giác ABC Vuông Tại A đường Cao AH ở trên sẽ giúp ích cho bạn trong việc nắm vững các kiến thức cơ bản về tam giác vuông và đường cao, từ đó giúp bạn dễ dàng áp dụng vào các bài toán và trở thành một tay toán giỏi. Cảm ơn bạn đã theo dõi bài viết của chúng tôi!