Tam giác vuông là một trong những hình học cơ bản trong toán học, và đường cao là một khái niệm quan trọng trong việc tính toán diện tích của tam giác. Tuy nhiên, để tính được đường cao của một tam giác vuông không phải là điều đơn giản. Trong bài viết này, chúng ta sẽ cùng Dapanchuan.com tìm hiểu về định lý, tính chất cũng như cách tính đường cao trong tam giác vuông, giúp bạn hiểu rõ hơn về khái niệm này và ứng dụng trong các bài toán hình học và toán học ứng dụng.
Đường cao trong tam giác vuông là gì?
Đường cao trong một tam giác vuông là đoạn thẳng nối đỉnh của góc vuông với đối diện của nó trên cạnh huyền. Nó được gọi là đường cao vì đó là đường đi từ đỉnh của góc vuông xuống đối diện của nó, và đồng thời cũng là đường cao của hình chiếu vuông góc của đỉnh đó lên cạnh đối diện. Đường cao trong một tam giác vuông cũng là bán kính của đường tròn nội tiếp của tam giác.
Định lý về đường cao trong tam giác vuông
Định lý đường cao trong tam giác vuông là một trong những định lý quan trọng trong hình học tam giác và được sử dụng rộng rãi trong các bài toán liên quan đến tam giác vuông.
Định lý đường cao trong tam giác vuông nói rằng: “Trong một tam giác vuông, đường cao còn là trung bình hình học và trung vị của cạnh huyền.”
Cụ thể hơn, giả sử trong tam giác vuông ABC có cạnh huyền BC, đường cao AH hạ xuống cạnh AB, và gọi M là trung điểm của cạnh BC. Khi đó, ta có:
- Độ dài đường cao AH bằng tích của độ dài cạnh huyền BC và độ dài cạnh góc vuông AB, chia cho độ dài đoạn thẳng AC: AH = (BC x AB) / AC
- Độ dài đường cao AH bằng độ dài đoạn thẳng BM: AH = BM = MC
- Độ dài đường cao AH cũng là trung bình cộng của hai cạnh góc vuông AB và BC: AH = (AB + BC) / 2
Định lý đường cao trong tam giác vuông là một công cụ quan trọng trong việc tính toán các thông số của tam giác vuông, cũng như trong việc giải quyết các bài toán hình học liên quan đến tam giác vuông.
Tính chất của đường cao trong tam giác vuông
Tam giác vuông là một loại tam giác đặc biệt có một góc vuông. Điều này dẫn đến các tính chất đặc biệt của đường cao trong tam giác vuông. Những tính chất này rất hữu ích trong quá trình giải các bài tập và cũng có ứng dụng trong cuộc sống. Sau đây là các tính chất cần ghi nhớ về đường cao trong tam giác vuông:
- Tính chất thứ nhất: Trong tam giác vuông, tích của độ dài đường cao với độ dài cạnh huyền tương ứng bằng tích của hai độ dài cạnh góc vuông trong tam giác.
- Tính chất thứ hai: Trong tam giác vuông, bình phương của độ dài cạnh góc vuông bằng tích của độ dài cạnh huyền và độ dài đường cao tương ứng chiếu lên cạnh huyền.
- Tính chất thứ ba: Trong tam giác vuông, bình phương của độ dài đường cao trên cạnh huyền bằng tích của độ dài hai hình chiếu của hai cạnh góc vuông lên cạnh huyền.
- Tính chất thứ tư: Trong tam giác vuông, nghịch đảo của bình phương mỗi cạnh góc vuông bằng nghịch đảo của bình phương độ dài đường cao.
Cách tính đường cao trong tam giác vuông
Dựa vào công thức tính cạnh cùng đường cao trong tam giác vuông, ta có công thức tính đường cao trong dạng tam giác vuông như sau:
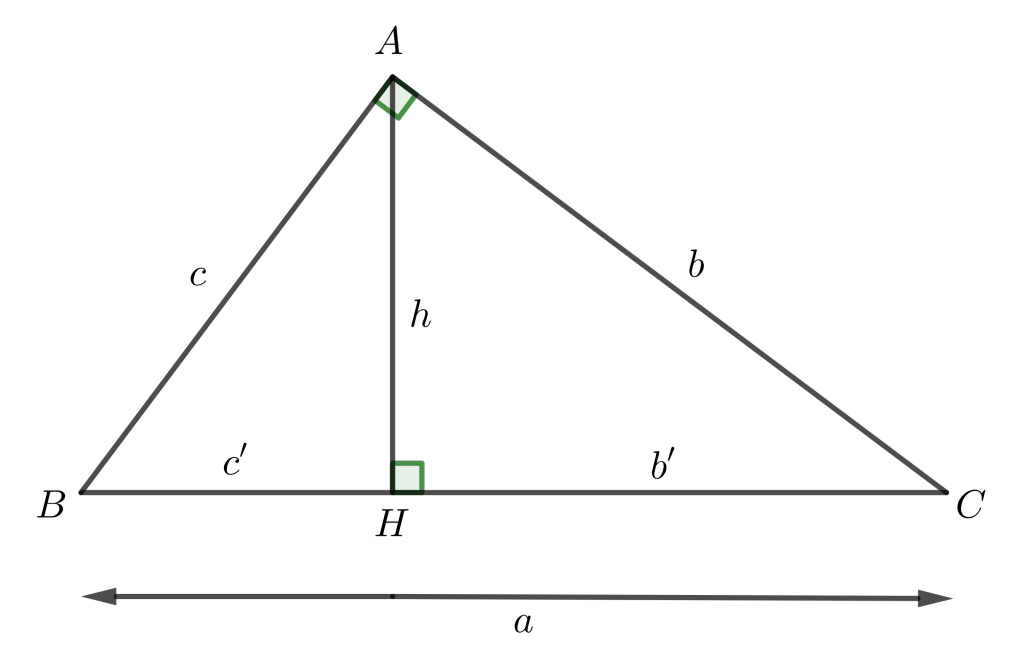
- a² = b² – c²
- b² = a.b′ và c²= a.c′
- a.h= b.c
- h²= b′.c′
- 1/b²=1/b²+1/c²
Trong đó:
- a, b, c: độ dài các cạnh thuộc tam giác vuông.
- b’: đường chiếu của cạnh b tương ứng trên cạnh huyền.
- c’: đường chiếu của cạnh c tương ứng trên cạnh huyền.
- h: đường cao hạ xuống từ đỉnh góc vuông.
Bài tập liên quan đến đường cao trong tam giác vuông
1. Cho hình △ABC vuông tại A có đường cao AH (H ∊ BC), biết BH= 9m, BC= 25m. Tính độ dài các đường cao trong △ABC?
Lời giải tham khảo:
H ∊ BC mà BH= 9m, BC= 25m
⇒ CH= 25 – 9 = 16 (m)
Áp dụng công thức tính cạnh và đường cao trong tam giác vuông ta có:
*) AH² = BH x CH = 9 x 16 = 144
⇒ AH = 12 (m)
*) AB² = BC x BH = 25 x 9 = 225
⇒ AB = 15 (m)
*) AC² = BC x CH = 25 x 16 = 400
⇒ AC = 20 (m)
Vậy độ dài 3 đường cao trong △ABC vuông tại A: AB, AC, AH lần lượt là 15m, 20m, 12m.
2. Cho tam giác ABC có góc vuông tại A, AB=24cm và AC=32cm. Đường trung trực của BC sẽ cắt AC, BC theo thứ tự là D và E. Tính DE.
Giải:
Xét trong tam giác vuông ABC, ta có:
BC2 = AB2+ AC2 ( theo định lý py-ta-go)
BC2 = 242+ 322
BC2 = 1600
BC = 40(cm)
EC = BC : 2 = 40 : 2 = 20(cm)
Xét theo tam giác vuông ACB và tam giác vuông ECD có:
Có góc A = góc E = 90o và góc C chung.
=> Tam giác ACB ∾ tam giác ECD
=> AC/EC = AB/ED
=> ED = AB.EC/AC = 15cm
Vậy ED = 15cm.
Như vậy, qua bài viết này chúng ta đã được tìm hiểu về các định lý, tính chất và cách tính đường cao trong tam giác vuông. Đường cao không chỉ là một khái niệm quan trọng trong hình học mà còn được ứng dụng rất nhiều trong các bài toán thực tế. Chắc chắn rằng, khi nắm vững kiến thức này, bạn sẽ có thể giải quyết được nhiều bài toán liên quan đến tam giác vuông một cách dễ dàng và hiệu quả hơn.