Hai đường thẳng song song là một trong những khái niệm cơ bản trong hình học. Khi đề cập đến chúng ta sẽ liên tưởng ngay đến các tính chất và phép toán liên quan, trong đó việc tìm số điểm chung của hai đường thẳng song song là một trong những vấn đề thường gặp. Chúng ta sẽ cùng Dapanchuan.com tìm hiểu về khái niệm hai đường thẳng song song cùng các tính chất liên quan khác ở bài viết sau.
Khái niệm 2 đường thẳng song song
Nếu hai đường thẳng nằm trên cùng một mặt phẳng và không có điểm chung nào, chúng được gọi là hai đường thẳng song song. Để chỉ sự song song của hai đường thẳng, ta sử dụng ký hiệu a//b. Trong hình học, nếu hai đường thẳng phân biệt thì chúng sẽ hoặc cắt nhau tại một điểm hoặc là song song với nhau.
Dấu hiệu nhận biết hai đường thẳng song song
Dưới đây là một số cách nhận biết hai đường thẳng song song trong một mặt phẳng:
- Nếu hai đường thẳng cắt một đường thẳng thứ ba và tạo ra cặp góc so le và bằng nhau thì hai đường thẳng đó song song.
- Nếu hai đường thẳng cắt một đường thẳng thứ ba và tạo ra cặp góc đồng vị và bằng nhau thì hai đường thẳng đó song song.
- Nếu hai đường thẳng cắt một đường thẳng thứ ba và tạo ra hai cặp góc ở trong cùng phía bù nhau thì hai đường thẳng đó song song.
Tính chất của 2 đường thẳng song song
Trong một mặt phẳng, các đặc điểm tính chất của hai đường thẳng song song khi bị cắt bởi một đường thẳng thứ ba là:
- Hai góc so le trong còn lại bằng nhau.
- Hai góc đồng vị và bằng nhau.
- Hai góc ở trong cùng phía bù nhau.
- Khi vẽ một đường thẳng qua một điểm nằm ngoài một đường thẳng đã cho. Chỉ có một đường thẳng duy nhất song song với đường thẳng đó.
Cách vẽ 2 đường thẳng song song
Để vẽ hai đường thẳng song song, ta có thể làm theo các bước sau:
- Vẽ đường thẳng AB cho trước.
- Chọn một điểm bất kỳ nằm ngoài đường thẳng AB và đặt tên là E.
- Vẽ đường thẳng MN đi qua điểm E sao cho đường thẳng MN vuông góc với đường thẳng AB.
- Vẽ đường thẳng CD đi qua điểm E sao cho đường thẳng CD vuông góc với đường thẳng MN.
- Khi đó, đường thẳng CD sẽ là đường thẳng song song với đường thẳng AB.
Cách chứng minh 2 đường thẳng song song
Cho hình tam giác ABC có đỉnh A là góc vuông. Qua điêm A, hãy vẽ đường thẳng Ax nằm song song với cạnh BC. Qua điểm C, hãy vẽ đường thẳng Cy nằm song song với cạnh AB. 2 đường thẳng Ax và Cy cắt tại điểm D. Nên tên những cặp cạnh song song trong hình tứ giác ADCB?
– Đầu tiên, chúng ta phải sử dụng eke để vẽ tứ giác ADBC. Trong tứ giác ADBC có:
- Cặp cạnh AD và BC song song với nhau
- Cặp cạnh AB và DC song song với nhau.
– Tiếp theo chúng ta sẽ chứng minh hai đường thẳng song song:
+ Xét vị trí của các cặp cạnh tạo bởi hai đường thẳng định chứng minh song song với 1 đường thẳng thứ 3 ( đồng vị, so le, trong cùng phía )
+ Dùng tính chất hình bình hành.
+ 2 đường thẳng nào cùng song song hoặc 2 đường thẳng cùng vuông góc với đường thẳng thứ 3 thì song song.
+ Dùng tính chất đường trung bình của tam giác, hình bình hành, hình thang.
+ Dùng định nghĩa về 2 đường thẳng song song.
+ Dùng kết quả của các đoạn thẳng tương ứng với các tỉ lệ để suy ra những đường thẳng song song tương ứng.
+ Định lý talet đảo: Dùng tính chất của đường thẳng đi qua trung điểm 2 cạnh bên hay đi qua trung điểm của 2 đường chéo của hình thang.
+ Dùng tính chất 2 cung bằng nhau của 1 đường tròn.
+ Dùng phương pháp chứng minh với phản chứng.
Số điểm chung của hai đường thẳng song song là?
Hai đường thẳng song song không có điểm chung nào cả, vì nếu có một điểm chung thì hai đường thẳng đó sẽ không còn song song nữa.
Tổng hợp dạng toán về hai đường thẳng song song
Sau đây là vài dạng toán liên quan đến 2 đường thẳng song song mà mọi người có thể tham khảo:
Dạng 1: Yêu cầu vẽ đường thẳng song song
Học sinh cần làm quen với các bước hướng dẫn vẽ hai đường thẳng song song ở phần trên. Sau đó, dựa vào yêu cầu của đề bài, học sinh tiến hành vẽ hai đường thẳng song song một cách chính xác.
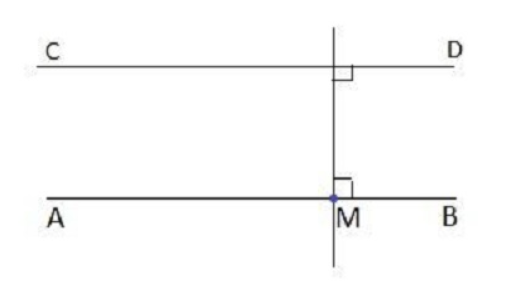
Ví dụ: Hãy vẽ đường thẳng AB đi qua điểm M và song song với đường thẳng CD.
Hướng dẫn giải:
- Bước 1: Vẽ đường thẳng MN đi qua M và vuông góc với CD.
- Bước 2: Vẽ đường thẳng AB đi qua M và vuông góc với MN.
Dạng 2: Chứng minh 2 đường thẳng song song
Phương pháp giải:Chúng sẽ căn cứ vào tính chất và dấu hiệu nhận biết của 2 đường thẳng song song để chứng minh theo yêu cầu của đề bài.
Ví dụ: Cho góc xOyˆ=α, điểm A được nằm trên tia Oy. Qua điểm A, vẽ tia Am. Tính số đo của OAmˆ để Am song song với Ox.
Hướng dẫn giải:
Ta xét hai trường hợp:
– Nếu tia Am thuộc miền trong của xOyˆ:
Để Am//Ox thì phải có A1ˆ=α (đồng vị)
Mà A1ˆ+A2ˆ=180∘ (kề bù)
–> A2ˆ=180∘−A1ˆ=180∘−α
Vậy OAmˆ=180∘−α
– Nếu tia Am thuộc miền ngoài của xOyˆ:
Để Am//Ox thì phải có A1ˆ=α (so le trong)
Vậy OAmˆ=α
Dạng 3: Tính toán số đo góc
– Phương pháp giải: Dựa vào tính chất, dấu hiệu nhận biết 2 đường thẳng song song. Chúng ta kết hợp với phép tính toán bình thường để tính số đo góc chuẩn xác.
– Ví dụ: Cho đường thẳng a và b cùng vuông góc với một đường thẳng c. Đồng thời c vuông góc với a tại M và vuông góc với đường thẳng b tại N. Có một đường thẳng m cắt a, b tại A và B. Biết số đo góc (ABN – MAB) = 40°. Vậy số đo góc BAM là bao nhiêu?
– Hướng dẫn giải:
Từ đề bài, ta có: a ⊥ c, b ⊥ c ⇒ a // b
⇒ ∠ABN + ∠MAB = 180° (2 góc trong cùng phía bù nhau)
Thông qua bài viết này, chúng ta đã tìm hiểu số điểm chung của hai đường thẳng song song là bao nhiêu và các phương pháp để chứng minh hai đường thẳng song song. Hi vọng bài viết sẽ giúp bạn hiểu rõ hơn về khái niệm này và có thể áp dụng vào các bài toán thực tế.