Cách tìm tiệm cận ngang là một kiến thức quan trọng trogn chương trình toán học lớp 12. Dạng bài toán này gặp ở rất nhiều đề thi và các bạn học sinh cần phải lưu ý. Trong bài viết hôm nay, Dapanchuan.com sẽ cung cấp các công thức và cách tìm tiệm cận ngang chuẩn nhất của đồ thị hàm số. Các bạn có thể tham khảo và áp dụng vào các bài toán liên quan đến tìm tiệm cận ngang.
Tiệm cận ngang là gì?
Nếu cho hàm số y = f(x) được xác định trên một trong các khoảng vô hạn (a; +∞), (-∞; b) hoặc (-∞; +∞), thì đường thẳng y = y0 được gọi là đường tiệm cận ngang hay tiệm cận ngang của đồ thị hàm số y = f(x) nếu nó thoả mãn ít nhất một trong các điều kiện sau: f(x) = y0 hoặc f(x) → y0 khi x tiến tới +∞ hoặc -∞.
Cách tìm tiệm cận ngang của đồ thị hàm số chuẩn nhất
Để tìm tiệm cận ngang của đồ thị hàm số y = f(x), ta thực hiện các bước sau:
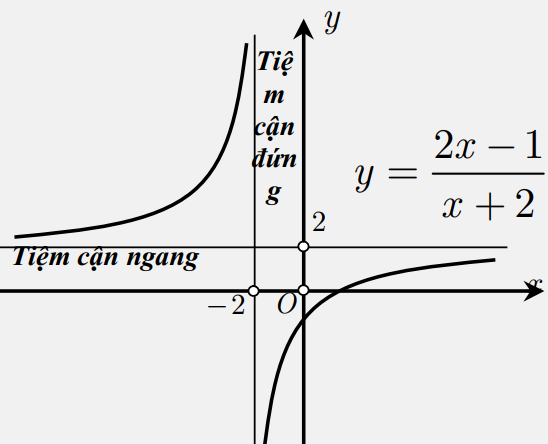
– Bước 1: Tìm giới hạn của hàm số f(x) khi x tiến tới +∞ hoặc -∞ bằng cách tính lim(f(x)) khi x tiến tới +∞ hoặc -∞. Nếu giới hạn này tồn tại và khác vô cùng thì đường thẳng y = y0, với y0 là giới hạn đó, là tiệm cận ngang của đồ thị.
– Bước 2: Nếu giới hạn khi x tiến tới +∞ hoặc -∞ không tồn tại hoặc bằng vô cùng, ta cần phân tích hàm số để tìm tiệm cận ngang. Các phương pháp phân tích phổ biến bao gồm:
- Xác định các điểm không liên tục của hàm số, ví dụ như các điểm phân thức, và kiểm tra xem có tồn tại tiệm cận ngang tại các điểm đó.
- Sử dụng các công thức lượng giác hoặc các định lý về giới hạn để xác định giá trị của hàm số khi x tiến tới các giá trị cụ thể.
- Phân tích đường cong đồ thị hàm số để xác định các đặc tính của nó, ví dụ như các điểm cực trị, điểm uốn, các đường tiệm cận khác, để từ đó suy ra tiệm cận ngang của đồ thị.
– Bước 3: Khi đã xác định được tiệm cận ngang của đồ thị hàm số, ta cần kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số để xác nhận rằng đường thẳng tìm được là tiệm cận ngang chính xác.
Công thức tính tiệm cận ngang
Sau đây là các công thức tính tiệm cận ngang của các hàm phân thức cụ thể:
Cách tìm tiệm cận ngang của hàm phân thức hữu tỉ
Để tính tiệm cận ngang của hàm phân thức hữu tỷ, ta cần phân tích đường cong đồ thị của hàm số và xác định giới hạn của nó khi x tiến tới vô cùng hoặc tiệm cận của nó tại các điểm khác.
– Có ba trường hợp chính xảy ra khi tính tiệm cận ngang của hàm phân thức hữu tỉ:
+ Nếu bậc của tử số lớn hơn bậc của mẫu số một đơn vị, tức là số mũ của biến x trong tử số lớn hơn số mũ của biến x trong mẫu số, thì đồ thị hàm số không có đường tiệm cận ngang.
Ví dụ: hàm số f(x) = (2x^2 + 3x + 1)/(x^2 – 5x + 6) không có tiệm cận ngang.
+ Nếu bậc của tử số bằng bậc của mẫu số, tức là số mũ của biến x trong tử số bằng số mũ của biến x trong mẫu số, thì đường thẳng y = hệ số của tử số/ hệ số của mẫu số là tiệm cận ngang của đồ thị.
Ví dụ: hàm số f(x) = (2x^2 – 5x + 1)/(x^2 – 3x + 2) có tiệm cận ngang y = 2.
+ Nếu bậc của tử số nhỏ hơn bậc của mẫu số một đơn vị, tức là số mũ của biến x trong tử số nhỏ hơn số mũ của biến x trong mẫu số, thì đường thẳng y = 0 là tiệm cận ngang của đồ thị.
Ví dụ: hàm số f(x) = (2x – 1)/(x^2 – x – 6) có tiệm cận ngang y = 0.
Chú ý rằng, các công thức này chỉ áp dụng cho các trường hợp đơn giản. Trong trường hợp phức tạp hơn, ta cần phân tích đường cong đồ thị hàm số và sử dụng các phương pháp khác để tính toán tiệm cận ngang.
Cách tìm tiệm cận ngang của hàm phân thức vô tỷ
Để tính tiệm cận ngang của hàm phân thức vô tỉ, ta cần phân tích đường cong đồ thị của hàm số và xác định giới hạn của nó khi x tiến tới vô cùng hoặc tiệm cận của nó tại các điểm khác.
– Có hai trường hợp chính xảy ra khi tính tiệm cận ngang của hàm phân thức vô tỷ y = (ax + b)/căn bậc hai của (cx^2 + dx + e), trong đó có a khác 0 và c khác 0:
+ Nếu c < 0 thì hàm phân thức không có tiệm cận ngang
+ Nếu c > 0 thì hàm phân thức có tiệm cận ngang là y = ± a / căn bậc 2 của c
Chú ý rằng, các công thức này chỉ áp dụng cho các trường hợp đơn giản. Trong trường hợp phức tạp hơn, ta cần phân tích đường cong đồ thị hàm số và sử dụng các phương pháp khác để tính toán tiệm cận ngang.
Cách tìm tiệm cận ngang bằng máy tính casio
Để sử dụng máy tính cầm tay để xác định tiệm cận ngang của một hàm số, chúng ta cần tính toán các giới hạn giá trị của hàm số:
- Đầu tiên, ta cần tính giá trị gần đúng của giới hạn y bằng cách chọn một giá trị x rất lớn, thường là x = 109, và tính giá trị của hàm số tại giá trị x này. Kết quả này sẽ cho chúng ta một ước lượng gần đúng của giới hạn y.
- Tương tự, để tính giá trị gần đúng của giới hạn y, chúng ta cần tính giá trị của hàm số tại một giá trị x rất nhỏ, thường là x = -109. Kết quả này sẽ cho chúng ta một ước lượng gần đúng của giới hạn y.
Ví dụ: để tìm tiệm cận ngang của hàm số y = (1-x)/(3x+1), ta có thể nhập hàm số này vào máy tính cầm tay, sau đó bấm phím CALC, nhập giá trị 109 và bấm dấu “=” để tính giá trị gần đúng của giới hạn y. Kết quả sẽ cho ta biết rằng hàm số này có một tiệm cận ngang là y = -13.
Cách tìm tiệm cận ngang trên bảng biến thiên
Một cách khác để xác định tiệm cận ngang của một hàm số là thông qua bảng biến thiên của nó. Quy trình thực hiện như sau:
- Tìm tập xác định của hàm số.
- Tính giới hạn của hàm số khi x tiến đến vô cùng (nếu hàm số có giới hạn vô cùng).
- Vẽ bảng biến thiên của hàm số.
- Xác định dấu của hàm số trên từng khoảng xác định trong bảng biến thiên.
- Xác định tiệm cận ngang của hàm số dựa trên dấu của hàm số khi x tiến đến vô cùng.
Ví dụ: Tìm tiệm cận ngang của hàm số y = (x^2 + 3)/(x + 1)
– Tập xác định của hàm số là R \ {-1}.
– Tính giới hạn của hàm số khi x tiến đến vô cùng: lim(x->+∞) (x^2 + 3)/(x + 1) = lim(x->+∞) (x^2 / (x + 1) + 3/(x + 1)) = +∞
– Vậy đường thẳng y = +∞ là một tiệm cận ngang của hàm số y = (x^2 + 3)/(x + 1) khi x tiến đến vô cùng.
Vẽ bảng biến thiên của hàm số:
| x | -1 | -∞ | +∞ |
|---|---|---|---|
| y’ | 0 | – | + |
| y | undef | – | + |
– Xác định dấu của hàm số trên từng khoảng xác định trong bảng biến thiên. Trên khoảng (-∞, -1), hàm số âm; trên khoảng (-1, +∞), hàm số dương.
– Xác định tiệm cận ngang của hàm số. Khi x tiến đến vô cùng, hàm số dương. Vậy đường thẳng y = +∞ là một tiệm cận ngang của hàm số y = (x^2 + 3)/(x + 1) khi x tiến đến vô cùng.
– Kết luận: Tiệm cận ngang của hàm số y = (x^2 + 3)/(x + 1) là đường thẳng y = +∞ khi x tiến đến vô cùng.
Một số dạng bài tập tìm tiệm cận ngang của đồ thị hàm số
Bài tập 1: Tìm tiệm cận ngang của hàm số y = 3x – 1
Giải:
– Vì đây là hàm số bậc nhất nên ta biết rằng nó có tiệm cận ngang là đường thẳng y = ax + b. Ta cần tìm a và b.
– Ta thấy rằng khi x tiến đến vô cùng, giá trị của hàm số sẽ tăng lên không giới hạn. Do đó, tiệm cận ngang của hàm số sẽ có hệ số góc a = 3.
– Để tìm hệ số b, ta có thể sử dụng điểm giao với trục y của đồ thị hàm số, tức là điểm (0, -1). Từ đó, ta có thể suy ra bằng cách:
y = ax + b
-1 = 3(0) + b
b = -1
– Vậy tiệm cận ngang của hàm số y = 3x – 1 là đường thẳng y = 3x – 1.
Bài tập 2: Tìm tiệm cận ngang của hàm số y = 2x^2 – 5x + 3
Giải:
– Vì đây là hàm số bậc hai nên ta biết rằng nó có tiệm cận ngang là đường thẳng y = ax + b. Ta cần tìm a và b.
– Khi x tiến đến vô cùng, giá trị của hàm số sẽ tăng lên không giới hạn nếu a > 0 hoặc giảm xuống không giới hạn nếu a < 0. Do đó, ta cần xét hệ số a để tìm ra tiệm cận ngang.
– Để tìm a, ta có thể sử dụng bảng biến thiên của hàm số:
| x | -∞ | 3/4 | +∞ |
|---|---|---|---|
| f(x) | +∞ | -1/8 | +∞ |
– Từ bảng biến thiên, ta thấy rằng hàm số có đỉnh là điểm (3/4, -1/8) và giá trị tại điểm đó là giá trị nhỏ nhất của hàm số. Khi x tiến đến vô cùng, giá trị của hàm số sẽ tăng lên không giới hạn nếu a > 0, do đó ta cần giả sử a > 0 và giải phương trình:
lim x→+∞ f(x)/(ax+b) = 0
lim x→+∞ (2x^2 – 5x + 3)/(ax + b) = 0
– Ta chia cả tử và mẫu của phân số cho x^2 và lấy giới hạn khi x tiến đến vô cùng để loại bỏ x
^2 trong tử:
lim x→+∞ (2 – 5/x + 3/x^2)/(a + b/x) = 0
– Vì a > 0, nên khi x tiến đến vô cùng, giá trị của b/x sẽ nhỏ hơn giá trị của a, do đó ta có thể bỏ qua thành phần b/x trong mẫu. Khi đó, ta có:
lim x→+∞ (2 – 5/x + 3/x^2)/(a) = 0
– Ta lấy giới hạn của phân số trên và dưới và được:
2/a = 0
– Vì vậy, a = 0 là không thể, ta kết luận rằng a phải dương.
– Để tìm b, ta có thể sử dụng công thức:
b = lim x→+∞ [f(x) – ax]
– Bằng cách sử dụng giá trị của a và điểm đỉnh, ta có:
b = lim x→+∞ [2x^2 – 5x + 3 – a(3/4)x – a(-1/8)]
b = lim x→+∞ [(8a/3)x^2 – (15a/4)x + (9a/4) + 3]
– Với a > 0, khi x tiến đến vô cùng, giá trị của hàm số sẽ tăng lên không giới hạn, do đó ta có thể bỏ qua các thành phần có bậc thấp hơn x^2. Khi đó, ta có:
b = lim x→+∞ [(8a/3)x^2]/x^2 = 8a/3
– Vậy, tiệm cận ngang của hàm số y = 2x^2 – 5x + 3 là đường thẳng y = 2x/3 – 4/3.
Lưu ý khi tìm tiệm cận ngang của đồ thị hàm số
Khi tìm tiệm cận ngang của đồ thị hàm số, ta cần lưu ý những điểm sau:
- Xác định tập xác định của hàm số trước khi tìm tiệm cận ngang, vì không phải hàm số nào cũng có tiệm cận ngang.
- Kiểm tra xem hàm số đó có bậc lớn hơn hai hay không, vì chỉ có hàm số bậc lớn hơn hai mới có thể có tiệm cận ngang.
- Nếu hàm số đó có tiệm cận ngang, ta cần xác định hệ số a và b của đường thẳng y = ax + b.
- Khi xác định hệ số a, ta cần xem xét dấu của a để xác định chiều của tiệm cận ngang. Nếu a > 0, tiệm cận ngang là đường thẳng tăng và nếu a < 0, tiệm cận ngang là đường thẳng giảm.
- Nếu hàm số đó có nhiều hơn một tiệm cận ngang, ta cần xác định chính xác từng tiệm cận ngang đó bằng cách sử dụng các phương pháp khác nhau như sử dụng bảng biến thiên, đạo hàm, hoặc phương pháp tính giới hạn.
- Khi tìm tiệm cận ngang, ta cần chú ý đến độ dốc của đường thẳng tiệm cận ngang và hình dạng của đồ thị hàm số, vì đây là các yếu tố quan trọng ảnh hưởng đến tính chất của hàm số.
Qua cách tìm tiệm cận ngang được chia sẻ ở bài viết trên, các bạn học sinh THPT có thể áp dụng ngay để giải các bài tập liên quan đến dạng toán này. Đây là kiến thức quan trọng mà các bạn phải nắm vững để giải quyết các bài thi một cách hiệu quả.