Công thức cách tính đường chéo trong hình lập phương là một trong những công thức khá phổ biến trong quá trình áp dụng bài tập hình học. Để hiểu rõ hơn về nền tảng cơ bản cho những bài tập liên quan đến đường chéo hình lập phương này mọi người cùng dapanchuan.com nhà tớ theo dõi bài viết ngay sau đây nhé!
Lý thuyết chung về hình lập phương
Hình lập phương là gì?
Hình lập phương được định nghĩa là khối đa diện đều có 6 mặt đều là các hình vuông bằng nhau. Trong đó có 12 cạnh bằng nhau và có tất cả 8 đỉnh, 3 cạnh gặp nhau tại 1 đỉnh và 4 đường chéo cắt nhau tại 1 điểm.
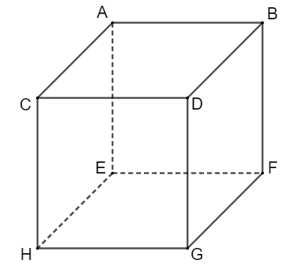
Cho hình lập phương như hình trên ta có:
+Bao gôm có 8 đỉnh như sau: đỉnh A, đỉnh C, đỉnh B, đỉnh D, đỉnh E, đỉnh F, đỉnh G, đỉnh H.
+12 cạnh bằng nhau bao gồm: AB = BD = DC = CA = CH = AE = DG = BF = FG = FE = EH = HG
+6 mặt là hình vuông băng nhau: ABCD, AEHC, BDGF, ABFE, EFGH, CDGH.
Tính chất hình lập phương
Các tính chất cần lưu ý về hình lập phương bao gồm:
+Hình lập phương có sáu mặt phẳng đối xứng và bằng nhau
+Hình lập phường có 12 cạnh bằng nhau
+Đường chéo của các mặt bên đều bằng nhau
+Đường chéo hình khối lập phương bằng nhau
Công thức cách tính đường chéo trong hình lập phương
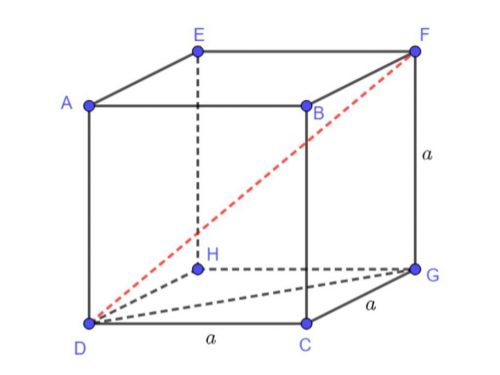
Xét hình lập phương ABCD. A’B’C’D’ cạnh a
Áp dụng định lý Pytago, ta tính được:
+ Đường chéo của 1 mặt là AC = a.căn 2
+ Đường chéo của hình lập phương AC’ = căn (AC^2 + CC’^2) = căn (2a^2 + a^2) = a.căn 3
Vậy đường chéo hình lập phương được thiết lập theo công thức là: a.căn 3

Dấu hiệu nhận biết hình lập phương
Trong mỗi đề bài, đôi khi người ta sẽ không lý giải và cho sẵn một hình lập phương mà phải chứng minh đó là hình lập phương sau đó mói đi tìm đường chéo. Chính vì thế mà dấu hiệu nhận biết về hình lập phương là một trong những kiến thức không thể thiếu, mọi người nắm kỹ kiến thức ngay sau đây nhé.
+Có 12 cạnh bằng nhau
+Có 6 mặt đều là hình vuông
Ngoài ra, xét về tổng thể bằng mắt thường thì ta sẽ thấy hình lập phương rất cân xứng với nhau
Trên đây là toàn bộ kiến thức về Công thức cách tính đường chéo trong hình lập phương dành đến bạn đọc. Mọi người cần nắm rõ công thức để áp dụng vào bài tập một cách nhanh chóng và chính xác nhật. Hi vọng các bạn sẽ thấy hình học thật dễ và thú vị hơn sau những đáp án mà nhà tớ đưa ra. Cảm ơn đã theo dõi hết bài viết!