Giao điểm 3 đường cao, tính chất của 3 đường cao trong tam giác là kiến thức quan trọng trong chương trình Toán học lớp 7. Kiến thức này được vận dụng nhiều để giải các bài tập về tam giác. Để hỗ trợ cho các bạn học sinh trong quá trình học tập, ôn tập. Dapanchuan.com có tổng hợp đầy đủ kiến thức về giao điểm 3 đường cao và các dạng toán vận dụng ở ngay phần sau đây.
Giao điểm 3 đường cao là gì?
Để tìm giao điểm ba đường cao của một tam giác, ta cần biết định nghĩa của đường cao trên tam giác đó. Đường cao trong tam giác là đoạn thẳng nối một đỉnh của tam giác với đường thẳng chứa cạnh đối diện. Giao điểm của đường cao với cạnh đối diện được gọi là chân đường cao.
Do đó, để tìm giao điểm ba đường cao của một tam giác ABC, ta cần vẽ tam giác và vẽ đường cao từ mỗi đỉnh của tam giác đến cạnh đối diện của nó. Khi đó, ta sẽ thu được ba đường cao và ba chân đường cao. Giao điểm của ba đường cao sẽ là một điểm duy nhất và được gọi là trục tâm của tam giác.
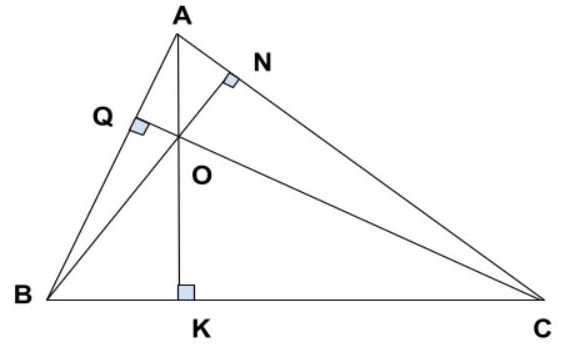
Tính chất 3 đường cao trong tam giác
Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác. Ví dụ: H là giao điểm ba đường cao của tam giác ABC thì H là trực tâm của tam giác ABC.
Các dạng toán liên quan đến giao điểm 3 đường cao
Dạng 1: Chứng minh 2 đường thẳng vuông góc với nhau:
– Phương pháp giải:
Để chứng minh hai đường thẳng vuông góc, ta có thể sử dụng phương pháp sử dụng tính chất trực tâm của tam giác. Cụ thể, nếu H là giao điểm của hai đường cao kẻ từ B và C của tam giác ABC thì AH vuông góc với BC.
Dạng 2: Bài toán về đường cao trong tam giác thường, tam giác cân, tam giác đều:
– Phương pháp giải:
- Sử dụng tính chất vuông góc của đường cao đối với cạnh đối diện của tam giác.
- Sử dụng định lý về tam giác cân, trong đó đường cao ứng với cạnh đáy của tam giác cân đồng thời là đường phân giác, đường trung tuyến và đường trung trực của tam giác đó.
- Sử dụng nhận xét rằng nếu hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường trung trực và đường cao) trùng nhau thì tam giác đó là tam giác cân.
Dạng 3: Chứng minh 3 đường thẳng đồng quy:
– Phương pháp giải:
Để chứng minh ba đường thẳng đồng quy, ta có thể sử dụng phương pháp sử dụng đường cao của tam giác. Nếu ba đường thẳng là ba đường cao của tam giác, thì chúng sẽ cùng đi qua trọng tâm của tam giác đó. Do đó, ta có thể chứng minh ba đường thẳng đồng quy bằng cách chứng minh rằng chúng cùng đi qua trọng tâm của tam giác.
Bài tập vận dụng liên quan đến giao điểm 3 đường cao
Bài 1: Cho ΔABC vuông cân tại B. Trên cạnh AB ta lấy điểm H, trên tia đối của tia BC ta lấy điểm D sao cho BD = BH. Chứng minh rằng:
a) DH ⊥ AC
b) CH ⊥ AD
– Hướng dẫn giải:
a) ΔABC vuông cân tại B nên ˆC=45∘
ΔBDH có ˆB=90∘ (theo giả thiết); BH = BD
Do đó ΔBDH vuông cân tại B, suy ra ˆD=45∘
ΔDIC có ˆD+ˆC=45∘+45∘=90∘
Vậy ˆDIC=90∘
Do đó DH ⊥ AC
b) ΔΔADC có AB ⊥ BC; DH ⊥AC
Suy ra H là trực tâm của ΔΔADC, suy ra CH cũng là đường cao của tam giác.
Do đó CH ⊥ AD.
Bài 2: Cho ΔABC có đường cao AH. Trên tia đối của tia AH, ta lấy điểm D sao cho đoạn AD = BC. Tại B ta kẻ đường thẳng BE ⊥ AB và BE = AB (E, C thuộc 2 nửa mặt phẳng đối nhau tính từ bờ là AB). Tại C ta kẻ đường thẳng CF⊥ AC và CF = AC (F, B thuộc 2 nửa mặt phẳng đối nhau tính từ bờ AC). Chứng minh rằng:
a) DC = BF, DC⊥BF
b) Ba đường thẳng DH, BF, CE đồng quy.
– Hướng dẫn giải:
a) ΔDAC và ΔBCF có:
DA = DC
AC = CF
ˆDAC=ˆBCF
⇒ΔDAC = ΔBCF
⇒ DC = BF; ˆC1=ˆF
Mà ˆC1+ˆC2=90∘⇒ˆF+ˆC2=90∘
Trong ΔCFI có: ˆF+ˆC2=90∘⇒ˆCIF=90∘. Vậy DC ⊥ BF
b) Tương tự, ta chứng minh ΔDAB = ΔCBE
⇒ˆB1=ˆE
Mà ˆB1+ˆB2=90∘⇒ˆE+ˆB2=90∘
Trong ΔEBG có: ˆE+ˆB2=90∘⇒ˆEBG=90∘. Vậy BD ⊥ CE
Trong ΔDBC có DH ⊥ BC; BI ⊥ AC; CG ⊥ AB. Vậy DH, BI, CG là 3 đường cao của ΔΔBDC
⇒ Vì vậy, DH, BI và CG đồng quy.
Bài 3: Cho ΔABC, gọi H là trực tâm thuộc ΔABC. Biết rằng AH = BC. Tính số đo góc ˆBAC.
– Hướng dẫn giải:
Trước tiên, ta thấy ˆA không thể bằng 90∘ vì nếu ˆA=90∘ thì trực tâm H sẽ trùng lên đỉnh A. Khi đó AH = 0.
– Ta xét các trường hợp :
+ Trường hợp 1: ˆA<90∘.
Xét ΔAHK và ΔBCK là 2 tam giác vuông có:
AH = BC
ˆB1=ˆA1
⇒ΔAHK = ΔBCK (cạnh huyền – góc nhọn)
⇒ AK = BK ⇒ΔABK vuông cân tại điểm K nên ˆBAC=45∘
+ Trường hợp 2: ˆA>90∘
Khi đó trực tâm H sẽ nằm ở ngoài tam giác. Tương tự ta sẽ chứng minh được ΔAHK = ΔBCK (cạnh huyền – góc nhọn) ⇒ HK = BK
Vậy ΔBKH vuông cân tại K ⇒ ˆBHC=45∘
Mà hai góc ˆBHC và ˆBAC có BA ⊥ HC, CA ⊥ HB, trong đó ˆBHC là góc tù ⇒ˆBHC+ˆBAC=180∘
⇒ˆBAC=180∘−45∘=135∘
Bài 4: Cho ΔΔABC, các đường thẳng chứa tia phân giác của 3 góc ngoài ΔABC sẽ cắt nhau tại 3 điểm là E, F, P (điểm E thuộc miền trong của góc ˆA, điểm F thuộc miền trong của góc ˆB và điểm P thuộc miền trong của góc ˆC). Chứng minh rằng:
a) Chứng minh 3 đường thẳng AE, BF, CP đồng quy tại điểm H.
b) Chứng minh 4 điểm E, F, P, H cách đều 3 đường thẳng AB, AC, BC
c) Chứng minh H là điểm trực tâm của ΔEFP.
– Hướng dẫn giải:
a) E là giao điểm của 2 đường phân giác của 2 góc ngoài ΔABC tại ˆB và ˆC. Vậy nên AE là tia phân giác bên trong ˆA
F là giao điểm của 2 đường phân giác của 2 góc ngoài ΔABC tại ˆA và ˆC nên BF là tia phân giác bên trong ˆB
P là giao điểm của 2 đường phân giác của 2 góc ngoài ΔABC tại ˆA và ˆB nên CP là tia phân giác bên trong ˆC
–>Suy ra AE, BF, CP là 3 đường phân giác bên trong của 3 góc trong ΔABC.
–>Do đó 3 đường thẳng AE, BF, CP đồng quy tại điểm H.
b) H là trực tâm thuộc ΔABC nên H sẽ cách đều 3 cạnh của ΔABC
Từ P hạ xuống PQ ⊥ AC và PI ⊥ BC vì P nằm trên đường phân giác ˆC và cách đều 2 cạnh, vậy PI = PQ.
Hạ xuống PS ⊥ AB, vì BP là phân giác của ˆABI –> PI = PS
Do đó PI = PQ = PS
Tương tự, ta chứng minh các điểm F, E cũng cách đều 3 cạnh của ΔΔABC
c) Tại A ta có ˆQAB và ˆBAC là 2 góc kề bù, trong đó AP sẽ là tia phân giác của ˆQAB, AE là tia phân giác của ˆBAC –> AP ⊥⊥ AE.
Tương tự tại B có ˆIBAvà ˆBAC là 2 góc kề bù, trong đó BP, BF là 2 tia phân giác
–>BF ⊥ BP.
Vậy trong ΔAFP có EA, FB là đường cao, H là giao điểm của EA, FB –> H là trực tâm trong ΔAFP.
Khái niệm giao điểm 3 đường cao ở bài viết trên đã giúp chúng ta hiểu rõ hơn về cấu trúc tam giác và các đường liên quan đến nó. Tuy nhiên, việc tìm giao điểm 3 đường cao không phải lúc nào cũng dễ dàng, đặc biệt là khi gặp các tam giác có đặc tính đặc biệt. Hy vọng bài viết này giúp ích cho bạn trong việc học tập và nghiên cứu các loại hình học trong toán học.