Phép tịnh tiến là một trong những phép biến đổi cơ bản trong hình học không gian và được sử dụng phổ biến trong đa dạng các ứng dụng, từ thiết kế đồ họa đến lập trình đồ họa. Trong bài viết này của Dapanchuan.com, chúng ta sẽ tìm hiểu về cách tìm ảnh của đường thẳng qua phép tịnh tiến và các bài tập vận dụng liên quan.
Cách tìm ảnh của đường thẳng qua phép tịnh tiến
Để tìm ảnh của một đường thẳng qua phép tịnh tiến, làm theo các bước sau:
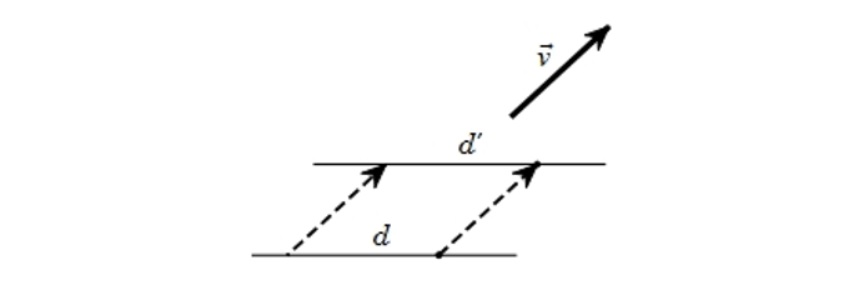
– Bước 1: Xác định phương trình của đường thẳng ban đầu
Nếu bạn đã có phương trình của đường thẳng, hãy bỏ qua bước này. Nếu không, bạn cần xác định phương trình của đường thẳng bằng cách sử dụng các điểm trên đường thẳng hoặc các thông số khác như độ dốc và điểm giao với trục tung.
– Bước 2: Xác định vector tịnh tiến
Vector tịnh tiến là vector di chuyển từ điểm ban đầu đến vị trí mới của đối tượng. Nó được xác định bởi các tham số (a, b), trong đó a là khoảng cách di chuyển theo trục x và b là khoảng cách di chuyển theo trục y.
– Bước 3: Áp dụng phép tịnh tiến để tìm ảnh của đường thẳng
Để tìm ảnh của đường thẳng, bạn cần áp dụng phép tịnh tiến cho mỗi điểm trên đường thẳng bằng cách thêm vector tịnh tiến vào tọa độ của nó. Điều này tương đương với việc di chuyển đường thẳng theo vector tịnh tiến.
Phương trình mới của đường thẳng được xác định bởi các điểm đã được dịch chuyển. Để tính toán phương trình mới, bạn có thể sử dụng hai điểm trên đường thẳng hoặc các thông số khác.
Ví dụ: Giả sử đường thẳng ban đầu có phương trình y = 2x + 1 và ta muốn dịch chuyển nó đi vị trí (3, 4). Ta có vector tịnh tiến là (3, 4).
Để tìm ảnh của đường thẳng, ta áp dụng phép tịnh tiến cho các điểm trên đường thẳng. Ví dụ, điểm (1, 3) sẽ được chuyển đến vị trí (1+3, 3+4) = (4, 7). Tương tự, ta áp dụng phép tịnh tiến cho các điểm khác trên đường thẳng.
Kết quả là phương trình mới của đường thẳng sau khi tịnh tiến được xác định bởi các điểm đã được dịch chuyển, chẳng hạn như y = 2x + 3.
Bài tập vận dụng cách tìm ảnh của đường thẳng qua phép tịnh tiến
– Bài tập 1: Tìm ảnh của đường thẳng y = 2x + 1 qua phép tịnh tiến T(3, 4).
Giải:
Đường thẳng ban đầu có phương trình y = 2x + 1.
Vector tịnh tiến T(3, 4).
Để tìm ảnh của đường thẳng, ta áp dụng phép tịnh tiến cho các điểm trên đường thẳng.
Ví dụ, điểm (1, 3) sẽ được chuyển đến vị trí (1+3, 2*1+1+4) = (4, 7).
Tương tự, ta áp dụng phép tịnh tiến cho các điểm khác trên đường thẳng.
Kết quả là phương trình mới của đường thẳng sau khi tịnh tiến được xác định bởi các điểm đã được dịch chuyển, chẳng hạn như y = 2x + 3.
Vậy, ảnh của đường thẳng y = 2x + 1 qua phép tịnh tiến T(3, 4) là y = 2x + 3.
– Bài tập 2: Tìm ảnh của đường thẳng 2x – 3y + 4 = 0 qua phép tịnh tiến T(-2, 5).
Giải:
Đường thẳng ban đầu có phương trình 2x – 3y + 4 = 0.
Vector tịnh tiến T(-2, 5).
Để tìm ảnh của đường thẳng, ta áp dụng phép tịnh tiến cho các điểm trên đường thẳng.
Điểm trên đường thẳng có thể được xác định bằng cách giải phương trình đường thẳng.
2x – 3y + 4 = 0
<=> y = (2/3)x + 4/3
Vậy, mọi điểm trên đường thẳng đều có dạng (x, (2/3)x + 4/3).
Áp dụng phép tịnh tiến, ta có:
(x’, y’) = (x-2, y+5) = (x-2, (2/3)x + 19/3)
Phương trình mới của đường thẳng sau khi tịnh tiến có thể được xác định bằng cách sử dụng hai điểm trên đường thẳng đã được dịch chuyển.
Ví dụ, điểm (0, 4/3) được dịch chuyển đến vị trí (-2, 4/3+5) = (-2, 23/3).
Tương tự, điểm (3, 10/3) được dịch chuyển đến vị trí (3-2, 10/3+5) = (1, 25/3).
Khi đó, ta có hai điểm trên đường thẳng đã được dịch chuyển là (-2, 23/3) và (1, 25/3).
Ta có thể tính được phương trình mới của đường thẳng bằng cách sử dụng hai điểm này.
Phương trình đường thẳng đi qua hai điểm (-2, 23/3) và (1, 25/3) có thể được xác định bằng cách giải hệ phương trình:
(-2)a + b = 23/3
(1)a + b = 25/3
Giải hệ phương trình này, ta được a = 2/3 và b = 19/3.
Vậy, phương trình mới của đường thẳng sau khi tịnh tiến là 2x – 3y + 10 = 0.
– Bài tập 3: Tìm ảnh của đường thẳng y = -x + 2 qua phép tịnh tiến T(2, -3).
Giải:
Đường thẳng ban đầu có phương trình y = -x + 2.
Vector tịnh tiến T(2, -3).
Để tìm ảnh của đường thẳng, ta áp dụng phép tịnh tiến cho các điểm trên đường thẳng.
Ví dụ, điểm (1, 1) sẽ được chuyển đến vị trí (1+2, -1+2-3) = (3, -2).
Tương tự, ta áp dụng phép tịnh tiến cho các điểm khác trên đường thẳng.
Kết quả là phương trình mới của đường thẳng sau khi tịnh tiến được xác định bởi các điểm đã được dịch chuyển, chẳng hạn như y = -x + 4.
Vậy, ảnh của đường thẳng y = -x + 2 qua phép tịnh tiến T(2, -3) là y = -x + 4.
– Bài tập 4: Tìm ảnh của đường thẳng x + y = 3 qua phép tịnh tiến T(4, 2).
Giải:
Đường thẳng ban đầu có phương trình x + y = 3.
Vector tịnh tiến T(4, 2).
Để tìm ảnh của đường thẳng, ta áp dụng phép tịnh tiến cho các điểm trên đường thẳng.
Ví dụ, điểm (1, 2) sẽ được chuyển đến vị trí (1+4, 2+2) = (5, 4).
Tương tự, ta áp dụng phép tịnh tiến cho các điểm khác trên đường thẳng.
Kết quả là phương trình mới của đường thẳng sau khi tịnh tiến được xác định bởi các điểm đã được dịch chuyển, chẳng hạn như x + y = 7.
Vậy, ảnh của đường thẳng x + y = 3 qua phép tịnh tiến T(4, 2) là x + y = 7.
– Bài tập 5: Tìm ảnh của đường thẳng 3x + 2y = 1 qua phép tịnh tiến T(-2, 2).
Giải:
Đường thẳng ban đầu có phương trình 3x + 2y = 1.
Vector tịnh tiến T(-2, 2).
Để tìm ảnh của đường thẳng, ta áp dụng phép tịnh tiến cho các điểm trên đường thẳng.
Ví dụ, điểm (-1, 1/2) sẽ được chuyển đến vị trí (-1-2, 1/2+2) = (-3, 5/2).
Tương tự, ta áp dụng phép tịnh tiến cho các điểm khác trên đường thẳng.
Kết quả là phương trình mới của đường thẳng sau khi tịnh tiến được xác định bởi các điểm đã được dịch chuyển, chẳng hạn như 3x + 2y = 13.
Vậy, ảnh của đường thẳng 3x + 2y = 1 qua phép tịnh tiến T(-2, 2) là 3x + 2y = 13.
– Bài tập 6: Tìm ảnh của đường thẳng y = 2x – 1 qua phép tịnh tiến T(3, -4).
Giải:
Đường thẳng ban đầu có phương trình y = 2x – 1.
Vector tịnh tiến T(3, -4).
Để tìm ảnh của đường thẳng, ta áp dụng phép tịnh tiến cho các điểm trên đường thẳng.
Ví dụ, điểm (0, -1) sẽ được chuyển đến vị trí (0+3, -1-4) = (3, -5).
Tương tự, ta áp dụng phép tịnh tiến cho các điểm khác trên đường thẳng.
Kết quả là phương trình mới của đường thẳng sau khi tịnh tiến được xác định bởi các điểm đã được dịch chuyển, chẳng hạn như y = 2x – 9.
Vậy, ảnh của đường thẳng y = 2x – 1 qua phép tịnh tiến T(3, -4) là y = 2x – 9.
– Bài tập 7: Tìm ảnh của đường thẳng 2x – y + 4 = 0 qua phép tịnh tiến T(-1, 3).
Giải:
Đường thẳng ban đầu có phương trình 2x – y + 4 = 0.
Vector tịnh tiến T(-1, 3).
Để tìm ảnh của đường thẳng, ta áp dụng phép tịnh tiến cho các điểm trên đường thẳng.
Ví dụ, điểm (-2, 0) sẽ được chuyển đến vị trí (-2-1, 0+3) = (-3, 3).
Tương tự, ta áp dụng phép tịnh tiến cho các điểm khác trên đường thẳng.
Kết quả là phương trình mới của đường thẳng sau khi tịnh tiến được xác định bởi các điểm đã được dịch chuyển, chẳng hạn như 2x – y – 2 = 0.
Vậy, ảnh của đường thẳng 2x – y + 4 = 0 qua phép tịnh tiến T(-1, 3) là 2x – y – 2 = 0.
Như vậy, thông qua bài viết này, chúng ta đã học được cách tìm ảnh của đường thẳng qua phép tịnh tiến. Bằng cách áp dụng các kỹ thuật và công thức cơ bản, bạn có thể tính toán và xác định phương trình mới của đường thẳng sau khi áp dụng phép tịnh tiến như các bài tập vận dụng ở trên.