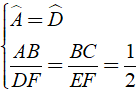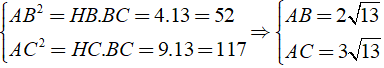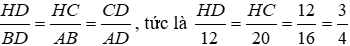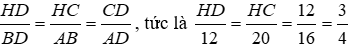Các trường hợp đồng dạng của tam giác vuông đóng vai trò quan trọng, mang lại những tính chất đặc trưng và ứng dụng hữu ích trong bộ môn toán lớp 8. Hãy cùng tham khảo qua nội dung bài viết sau đây của DapAnChuan.com để tìm hiểu chi tiết về các dạng toán này
Tam giác vuông đồng dạng là gì?
Tam giác vuông đồng dạng là một khái niệm toán học liên quan đến tính chất tương tự giữa các tam giác vuông. Hai tam giác vuông được coi là đồng dạng nếu các góc vuông tương ứng của chúng bằng nhau và tỉ lệ giữa độ dài các cạnh tương ứng cũng bằng nhau.
Hai tam giác vuông đồng dạng nếu
- Tam giác vuông này có góc nhọn bằng với góc nhọn của một tam giác vuông khác thì hai tam giác đồng dạng
- Hai cạnh tạo nên góc vuông này tỉ lệ tương ứng với hai cạnh tạo nên góc vuông của tam giác khác thì hai tam giác đó đồng dạng với nhau.
- Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỷ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia, thì được xem là 2 tam giác vuông đồng dạng
Tính chất đồng dạng giữa các tam giác vuông này cho phép ta áp dụng các phương pháp hình học để giải quyết các vấn đề liên quan đến các tam giác vuông trong toán học và các lĩnh vực khác.
Các trường hợp đồng dạng của tam giác vuông
Sau đây là thông tin chi tiết về các trường hợp đồng dạng của tam giác vuông, mọi người cùng tham khảo
Lý thuyết các trường hợp đồng dạng của tam giác vuông
Tam giác vuông là một trong những loại tam giác cơ bản và thường xuyên xuất hiện trong các bài toán hình học và toán học khác. Trong lý thuyết tam giác vuông, có một số trường hợp đặc biệt và quan trọng về đồng dạng mà bạn có thể quan tâm đến.
Trường hợp đồng dạng (Góc-Góc- Góc)
Để chứng minh rằng hai tam giác vuông đồng dạng, cần phải xác định các điều kiện tương đương đó là hai tam giác cần phải có hai góc bằng nhau và một cạnh tương ứng bằng nhau. Qua đó đảm bảo tỷ lệ giữa các cạnh và góc của hai tam giác là như nhau.
Trường hợp đồng dạng (Đỉnh-Đỉnh)
Để chứng minh sự đồng dạng giữa hai tam giác vuông, chúng ta cần xác định các điều kiện cần và đủ. Cụ thể, hai tam giác vuông này bằng với tam giác vuông kia được coi là đồng dạng nếu các đỉnh của chúng tương ứng với nhau.
Trường hợp đồng dạng (Cạnh-Góc-Cạnh)
Hai tam giác vuông được xem là đồng dạng khi chúng có cặp góc vuông tương đồng và cạnh kề tương ứng đồng nhau, cùng với một cặp cạnh tương ứng khác cũng đồng nhau. Điều này có nghĩa rằng tỷ lệ giữa các cạnh và góc trong hai tam giác vuông đồng dạng sẽ giống nhau, cho phép ta áp dụng các quy tắc hình học tương tự để giải quyết vấn đề và tính toán các đại lượng liên quan đến các tam giác này.
Trường hợp đồng dạng (Cạnh-Cạnh-Cạnh):
Hai tam giác vuông đồng dạng nếu độ dài của tất cả các cạnh tương ứng của chúng đồng nhau.
Hai tam giác vuông được coi là đồng dạng nếu tất cả các góc trong tam giác đầu tiên tương ứng với các góc trong tam giác thứ hai và các tỉ lệ giữa độ dài các cạnh tương ứng cũng bằng nhau. Nói cách khác, nếu tam giác vuông thứ nhất có các cạnh a,b,c và tam giác vuông thứ hai có các cạnh l, m,n bằng nhau, thì hai tam giác vuông đó đồng dạng.
Nhận biết các trường hợp đồng dạng của tam giác vuông
Để nhận biết được 2 tam giác vuông có tính đồng dạng với nhau thì các em cần tham khảo qua các yếu tố sau đây
- Về cạnh huyền và cạnh góc vuông: Nếu một cạnh huyền và một cạnh tạo thành góc vuông của một tam giác vuông có tỉ lệ bằng nhau với cạnh huyền và một cạnh tạo thành góc vuông của một tam giác vuông khác, thì hai tam giác vuông đó được coi là đồng dạng.
- Về tỷ lệ đường cao của 2 tam giác : Nếu tỷ lệ đường cao của 2 tam giác vuông bằng tỷ lệ đồng dạng của 2 tam giác đó, thì nó được xem là đồng dạng với nhau
- Tỷ số diện tích bằng bình phương tỷ số đồng dạng: Nếu tỷ lệ diện tích của 2 tam giác bằng bình phương tỷ lệ đồng dạng của 2 tam giác, thì nó được xem là đồng dạng với nhau
- Tỷ số hai đường phân giác tương ứng bằng tỉ số đồng dạng: Nếu tỷ hai đường phân giác bằng tỷ số đồng dạng của 2 tam giác, thì nó được xem là đồng dạng với nhau
- Tỷ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng: Nếu tỷ số hai đường truy tuyến của 2tam giác bằng tỷ số đồng dạng của 2 tam giác đó, thì nó được xem là đồng dạng với nhau
- Tỷ số chu vi của hai tam giác bằng tỉ số đồng dạng: Nếu tỷ số chu vi của 2 tam giác tỷ số đồng dạng của 2 tam giác, thì nó được xem là đồng dạng với nhau
Cách xác định hai tam giác vuông đồng dạng
Để chứng minh hai tam giác vuông có đồng dạng, bạn cần thực hiện các bước sau. Trước tiên, đo và so sánh các góc vuông của hai tam giác để xác định xem chúng có bằng nhau hay không. Sau đó, tiến hành đo và so sánh các cạnh tương ứng của tam giác để kiểm tra tỷ lệ giữa chúng có bằng nhau hay không.
>>> Xem thêm: Các trường hợp bằng nhau của tam giác vuông, bài tập có lời giải
Bài tập các trường hợp đồng dạng của tam giác vuông
Sau đây là bài tập vận dụng các trường hợp đồng dạng của tam giác vuông
Bài tập trắc nghiệm
BÀI 1: Nếu hai tam giác đồng dạng với nhau thì: Chọn phát biểu sai trong các phát biểu sau?
A. Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.
B. Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.
C. Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
D. Tỉ số các chu vi bằng 2 lần tỉ số đồng dạng.
Lời giải:
Nếu hai tam giác đồng dạng với nhau thì:
+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
+ Tỉ số các chu vi bằng tỉ số đồng dạng.
Đáp án D sai.
Chọn đáp án D.
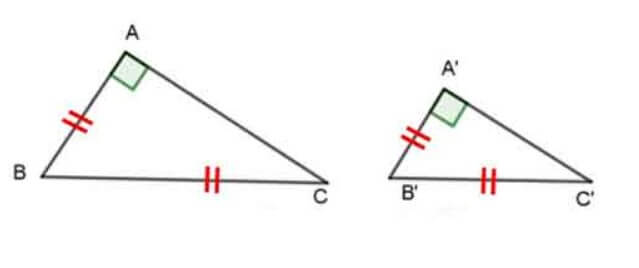
BÀI 2: Cho tam giác ABC có AB = 3cm; AC = 4cm và BC = 5cm. Tam giác MNP vuông tại M có MN = 6cm; MP = 8cm. Tìm khẳng định sai
A. Tam giác ABC là tam giác vuông
B. Δ ABC và ΔMNP đồng dạng với nhau
C. NP = 10 cm
D. Có hai phương án sai
Lời giải:
Ta có: AB2 + AC2 = BC2 ( 32 + 42 = 52 = 25)
Suy ra: tam giác ABC vuông tại A
Xét Δ ABC và Δ MNP có:
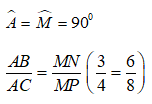
Suy ra: Δ ABC và ΔMNP đồng dạng với nhau.
Áp dụng định lí Pyta go vào tam giác MNP có:
NP2 = MN2 + MP2 = 62 + 82 = 100 nên NP = 10cm
Chọn đáp án D
BÀI 3: Cho ta giác ABC vuông tại A, kẻ AH vuông góc BC. Biết BH = 25 và HC = 36. Tính AH?
A. 18cm
B. 25cm
C. 20cm
D. 32cm
Lời giải:
Xét ΔAHB và ΔCHA có:
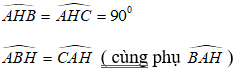
Suy ra: ΔAHB và ΔCHA đồng dạng với nhau ( g.g)
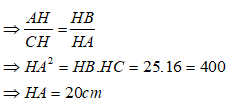
Chọn đáp án C
BÀI 4: Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm . Tam giác MNP đồng dạng với tam giác ABC và diện tích tam giác MNP là 96 cm2. Tính độ dài các cạnh của tam giác MNP?
A. 9cm, 12cm, 15cm
B. 12cm, 16cm ; 20cm
C. 6cm, 8cm, 10cm
D. Đáp án khác
Lời giải:
Ta có: AB2 + AC2 = BC2 (32 + 42 = 52
Suy ra: tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
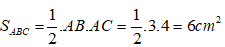
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
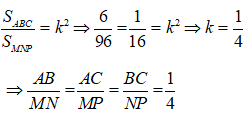
Thay số
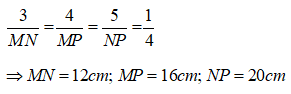
Chọn đáp án B
BÀI 5: Cho hai tam giác ABC và DEF có ˆA=ˆD=90° ,AB = 3cm, BC = 5cm, EF = 10cm, DF = 6cm. Chọn phát biểu đúng trong các phát biểu sau?
A. Δ ABC ∼ Δ DEF
B. Δ ABC ∼ Δ EDF
C. Δ ABC ∼ Δ DFE
D. Δ ABC ∼ Δ FDE
Lời giải:
Ta có:
⇒ Δ ABC ∼ Δ DFE ( c – g – c )
Chọn đáp án C.
BÀI 6: Cho tam giác vuông ABC vuông tại A, chân đường cao AH của tam giác ABC chia cạnh huyền BC thành hai đoạn thẳng BH = 4cm, HC = 9cm. Tính diện tích tam giác ABC?
A. SABC = 39cm2
B. SABC = 36cm2
C. SABC = 78cm2
D. SABC = 18cm2Lời giải:
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A
Ta có:
Vậy SABC = 1212AB.AC = 12.2√1312.213 .3√13313 = 39( cm2 )
Chọn đáp án A.
BÀI 7: Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Tính độ dài HD.
A. 12cm
B. 6cm
C. 9cm
D. 10cm
Lời giải
Tam giác ABC cân tại A nên BD = DC = 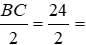
Theo định lý Py-ta-go, ta có AD2 = AC2 – DC2 = 202 – 122 = 162
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
góc CDH = góc ADB = 900
góc C1 = góc A1 (cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên
Suy ra HD = 9cm.
Đáp án cần chọn là: C
BÀI 8: Cho tam giác ABC vuông ở A, đường cao AH. Tính HB.HC bằng
A. AB2
B. B. AH2
C. C. AC2
D. D. BC2
Lời giải
Ta có: HAB + HAC = BAC = 900
Mà: HBA + HAB = 900 (2 góc phụ nhau)
⇒ góc HAC = góc HBA
Xét 2 tam giác vuông AHB và CHA ta có: góc HAC = góc HBA (cmt)
⇒ ΔAHB ~ ΔCHA (g – g)
⇒ 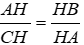
Đáp án cần chọn là: B
BÀI 9: Cho BH = 9cm, HC = 16cm. Tính diện tích của tam giác ABC.
A. 250cm2
B. B. 300cm2
C. C. 150cm2
D. D. 200cm2
Lời giải
Với BH = 9cm, HC = 16cm ⇒ BC = BH + HC = 9 + 16 = 25 cm
Ta có: AH2 = HB.HC (cmt)
⇒ AH2 = 9.16 = 144 ⇒ AH = 12cm
Nên diện tích tam giác ABC là SABC = 

Đáp án cần chọn là: C
Bài tập tự luận
BÀI 1: Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Độ dài AH là?
Lời giải
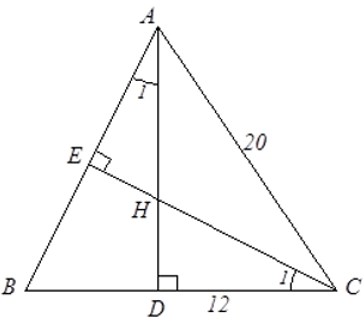
Tam giác ABC cân tại A nên BD = DC = 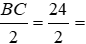
Theo định lý Py-ta-go, ta có AD2 = AC2 – DC2 = 202 – 122 = 162
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
Góc CDH= góc ADB=90°
Góc C1= Góc A1(cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên
Suy ra HD = 9cm ⇒ AH = AD – HD = 16 – 9 = 7cm
BÀI 2: Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Tính độ dài HD.
Lời giải:
Lời giải
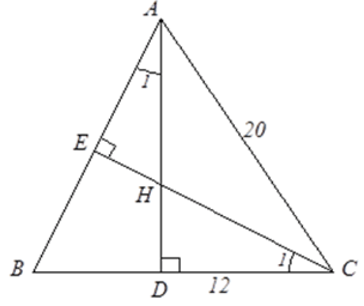
Tam giác ABC cân tại A nên BD = DC = 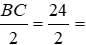
Theo định lý Py-ta-go, ta có AD2 = AC2 – DC2 = 202 – 122 = 162
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
Góc CDH=Góc ADB=90°
Góc C1=Góc A1 (cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên
Suy ra HD = 9cm.
BÀI 3: Cho tam giác ABC vuông ở A, đường cao AH. Tính HB.HC bằng?
Lời giải:
Lời giải
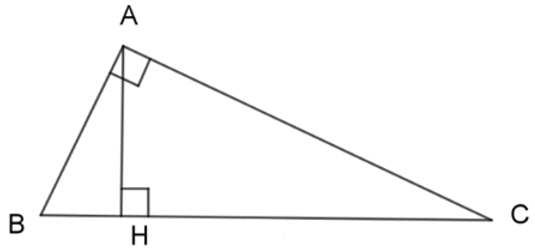
Ta có: Góc HAB+ góc HAC= góc BAC=90°
Mà: Góc HBA= góc HAB=90° (2 góc phụ nhau)
⇒ Góc HAC= Góc HBA
Xét 2 tam giác vuông AHB và CHA ta có: Góc HAC= góc HBA (chứng minh trên)
⇒ ΔAHB ~ ΔCHA (g – g)
⇒ 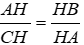
Lời giải

Ta có: Góc HAB+ góc HAC= góc BAC=90°
Mà: Góc HBA= Góc HAB=90° (2 góc phụ nhau)
⇒ Góc HAC= Góc HBA
Xét 2 tam giác vuông AHB và CHA ta có: Góc HAC= Góc HBA(cmt)
⇒ ΔAHB ~ ΔCHA (g – g)
⇒ 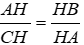
BÀI 4: Bóng của cột điện trên mặt đất có độ dài là 4,5m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 0,6m. Tính chiều cao của cột điện.
Lời giải
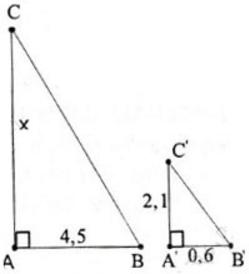
Giả sử cột điện là AC, có bóng trên mặt đất là AB.
Thanh sắt là A’C’, có bóng trên mặt đất là A’B’.
Vì cột điện và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A’B’C’ đều là tam giác vuông.
Vì cùng một thời điểmc tia sáng chiếu nên ta suy ra góc ACB= Góc A’C’B’
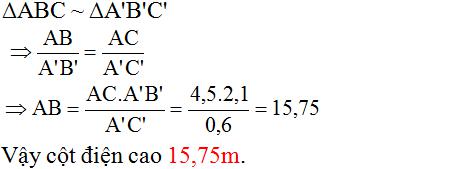
BÀI 5: Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Tính độ dài HD.
Lời giải

Tam giác ABC cân tại A nên BD = DC = 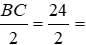
Theo định lý Py-ta-go, ta có AD2 = AC2 – DC2 = 202 – 122 = 162
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
Góc CDH= Góc ADB=90°�
Góc C1= Góc A1 (cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên
Suy ra HD = 9cm.
Qua nội dung bài viết trên, hy vọng giúp các học sinh lớp 8 hiểu sâu hơn về các trường hợp đồng dạng của tam giác vuông và đã bắt đầu áp dụng quy tắc này vào bài làm. Chúc các em thành công!