Cách tìm tập xác định của hàm số lớp 10 hiện nay sẽ có 2 cách bao gồm: Xét biểu thức f(x) có nghĩa hay không và Sử dụng các định lý về tập xác định của hàm số. Vậy trong bài viết này, hãy cùng DapAnChuan.Com tìm hiểu chi tiết về hai cách trên để có thể áp dụng vào việc tìm tập xác định của hàm số lớp 10 một cách nhanh chóng và đơn giản nhất!
Tập xác định của hàm số là gì?
Trong toán học, tập xác định (còn gọi là miền xác định, hay miền) của một hàm số là tập hợp các giá trị của biến số làm cho hàm số đó có nghĩa. Như vậy hàm số sẽ cho một giá trị kết quả cho mọi biến số nằm trong miền xác định này.
Tập xác định thường được ký hiệu là D.
Ý nghĩa của tập xác định của hàm số là để xác định xem hàm số đó có thể được xác định tại một điểm hay không. Nếu một điểm x không thuộc tập xác định của hàm số, thì hàm số sẽ không có nghĩa tại điểm đó. Dưới đây là một số cách để tìm tập xác định của hàm số:
Dùng quy tắc đơn giản:
- Nếu hàm số là một đa thức, thì tập xác định của hàm số là tất cả các số thực.
- Nếu hàm số là một số mũ, thì tập xác định của hàm số là tất cả các số thực x sao cho a > 0 và a ≠ 1.
- Nếu hàm số là một hàm lượng giác, thì tập xác định của hàm số là tất cả các số thực x.
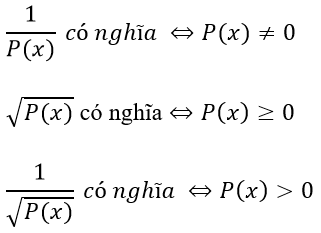
Dùng phương trình:
- Nếu hàm số là một hàm số chứa một số lượng tử, thì cần tìm tất cả các giá trị của biến số làm cho số lượng tử có nghĩa.
- Nếu hàm số là một hàm số chứa một hàm số khác, thì cần tìm tập xác định của hàm số khác.
Dùng biểu đồ:
- Nếu hàm số có thể được biểu diễn bằng một đồ thị, thì tập xác định của hàm số là tập hợp tất cả các điểm nằm trên đồ thị.
Cách tìm tập xác định của hàm số lớp 10
Tập xác định của hàm số là tập hợp tất cả các giá trị của biến số x mà hàm số f(x) nhận được. Tập xác định của hàm số lớp 10 là tập hợp các giá trị của biến số x làm cho hàm số đó có nghĩa. Như vậy, hàm số sẽ cho một giá trị kết quả cho mọi biến số nằm trong miền xác định này.
Cách tìm tập xác định của hàm số lớp 10 rất đơn giản, chỉ cần xét các điều kiện cho phép hàm số có nghĩa. Từ các điều kiện đó, ta suy ra tập hợp các giá trị của biến x sao cho hàm số có nghĩa. Để tìm tập xác định của hàm số lớp 10, ta cần xem xét các điều kiện sau:
- Nếu hàm số được biểu diễn dưới dạng y = f(x), ta cần xem xét xem biểu thức f(x) có chia hết cho 0 hay không. Nếu có, thì x không thuộc tập xác định của hàm số.
- Nếu hàm số được biểu diễn dưới dạng y = f(x), ta cần xem xét xem biểu thức f(x) có nghĩa hay không. Nếu có, thì x thuộc tập xác định của hàm số.
Ví dụ:
Hàm số f(x) = x^2 + 1
Trong hàm số này, không có bất kỳ điều kiện nào cho phép hàm số không có nghĩa. Do đó, tập xác định của hàm số là D = (-∞; +∞).
- Hàm số f(x) = 1/x
Trong hàm số này, nếu x = 0 thì hàm số không có nghĩa. Do đó, tập xác định của hàm số là D = (-∞; 0) ∪ (0; +∞).
- Hàm số f(x) = √x
Trong hàm số này, nếu x < 0 thì hàm số không có nghĩa. Do đó, tập xác định của hàm số là D = [0; +∞).
- Hàm số f(x) = sin(x)
Trong hàm số này, hàm số có nghĩa với mọi giá trị của x. Do đó, tập xác định của hàm số là D = (-∞; +∞).
- Hàm số f(x) = |x|
Trong hàm số này, hàm số có nghĩa với mọi giá trị của x. Do đó, tập xác định của hàm số là D = (-∞; +∞).
Một số dạng bài tập tìm tập xác định của hàm số lớp 10:
- Tìm tập xác định của hàm số f(x) = ax^2 + bx + c, với a, b, c là các số thực.
- Tìm tập xác định của hàm số f(x) = √(ax^2 + bx + c), với a, b, c là các số thực.
- Tìm tập xác định của hàm số f(x) = sin(ax + b), với a, b là các số thực.
- Tìm tập xác định của hàm số f(x) = |ax + b|, với a, b là các số thực.
Tổng hợp bài tập tìm tập xác định của hàm số lớp 10
Dạng 1: Hàm số bậc nhất
Hàm số bậc nhất có dạng y = ax + b, với a và b là các số thực. Tập xác định của hàm số bậc nhất là tất cả các số thực x sao cho biểu thức ax + b có nghĩa.
Ví dụ: Tìm tập xác định của hàm số y = 2x + 3.
Lời giải:
Biểu thức 2x + 3 có nghĩa khi và chỉ khi x không phải là số ảo. Suy ra, tập xác định của hàm số là D = (-∞; +∞).
Dạng 2: Hàm số bậc hai
Hàm số bậc hai có dạng y = ax^2 + bx + c, với a, b, c là các số thực. Tập xác định của hàm số bậc hai là tất cả các số thực x sao cho biểu thức ax^2 + bx + c có nghĩa.
Ví dụ: Tìm tập xác định của hàm số y = x^2 – 3.
Lời giải:
Biểu thức x^2 – 3 có nghĩa khi và chỉ khi x không phải là số ảo. Suy ra, tập xác định của hàm số là D = (-∞; +∞).

Dạng 3: Hàm số phân thức
Hàm số phân thức có dạng y = \frac{P(x)}{Q(x)}, với P(x) và Q(x) là các đa thức. Tập xác định của hàm số phân thức là tất cả các số thực x sao cho biểu thức Q(x) khác 0.
Ví dụ: Tìm tập xác định của hàm số y = \frac{x^2 – 1}{x – 1}.
Lời giải:
Biểu thức x – 1 khác 0 khi và chỉ khi x không phải là 1. Suy ra, tập xác định của hàm số là D = (-∞; 1) ∪ (1; +∞).
Dạng 4: Hàm số căn thức
Hàm số căn thức có dạng y = \sqrt{P(x)}, với P(x) là đa thức. Tập xác định của hàm số căn thức là tất cả các số thực x sao cho P(x) >= 0.
Ví dụ: Tìm tập xác định của hàm số y = \sqrt{x^2 + 1}.
Lời giải:
Biểu thức x^2 + 1 >= 0 khi và chỉ khi x >= -1 và x <= 1. Suy ra, tập xác định của hàm số là D = [-1; 1].
Dạng 5: Hàm số lượng giác
Hàm số lượng giác có dạng y = a sin(bx + c) + d, với a, b, c, d là các số thực. Tập xác định của hàm số lượng giác là tất cả các số thực x.
Ví dụ: Tìm tập xác định của hàm số y = sin(x).
Lời giải:
Hàm số sin(x) có nghĩa với mọi giá trị của x. Suy ra, tập xác định của hàm số là D = (-∞; +∞).
Dạng 6: Hàm số kết hợp
Hàm số kết hợp là hàm số được tạo thành từ hai hoặc nhiều hàm số. Tập xác định của hàm số kết hợp được xác định theo các quy tắc sau:
- Nếu hàm số kết hợp được tạo thành từ hai hàm số số học, thì tập xác định của hàm số kết hợp là giao của hai tập xác định của hai hàm số đó.
- Nếu hàm số kết hợp được tạo thành từ hai hàm số lượng giác, thì tập xác định của hàm số kết hợp là giao của hai tập xác định của hai hàm số đó.
- Nếu hàm số kết hợp được tạo thành từ một hàm số số học và một hàm số lượng giác, thì tập xác định của hàm số kết hợp là giao của tập xác định của hàm số số học và tập xác định của hàm số lượng giác.
Ví dụ: Tìm tập xác định của hàm số y = 2 sin(x) + 3x.
Lời giải:
Tập xác định của hàm số y = 2 sin(x) là (-∞; +∞). Tập xác định của hàm số y = 3x là (-∞; +∞). Suy ra, tập xác định của hàm số y = 2 sin(x)
Bài tập trắc nghiệm tìm tập xác định hàm số lớp 10
Dưới đây là một số ví dụ về các dạng bài tập trắc nghiệm để tìm tập xác định của hàm số trong lớp 10:
Ví dụ 1: Hàm số đơn giản Hãy xem xét hàm số f(x) = x^2 – 4x + 3. Hỏi tập xác định của hàm số này là gì?
A. Tất cả các số nguyên.
B. Tất cả các số thực.
C. Các số nguyên x sao cho x ≠ 0.
D. Các số thực x sao cho x ≠ 2.
Lời giải: Tập xác định của hàm số f(x) = x^2 – 4x + 3 là tất cả các số thực, vì bạn có thể thay bất kỳ giá trị nào cho x và tính được giá trị tương ứng của hàm số. Đáp án là B.
Ví dụ 2: Hàm số với biểu thức chia Xét hàm số f(x) = 1/(x – 2). Hỏi tập xác định của hàm số này là gì?
A. Tất cả các số thực.
B. Tất cả các số thực ngoại trừ x = 2.
C. Tất cả các số thực trừ x = 0.
D. Các số nguyên.
Lời giải: Tập xác định của hàm số f(x) = 1/(x – 2) là tất cả các số thực ngoại trừ x = 2, vì chia cho 0 (x – 2 = 0) không xác định. Đáp án là B.
Ví dụ 3: Hàm số với căn bậc 2 Xét hàm số f(x) = √(x + 5). Hỏi tập xác định của hàm số này là gì?
A. Tất cả các số nguyên.
B. Tất cả các số thực.
C. Các số thực x sao cho x > -5.
D. Các số thực x sao cho x > 5.
Lời giải: Tập xác định của hàm số f(x) = √(x + 5) là các số thực x sao cho x + 5 phải lớn hơn hoặc bằng 0 (vì căn bậc 2 của số âm không xác định trong tập số thực). Vì vậy, tập xác định là các số thực x sao cho x >= -5. Đáp án là C.
Ví dụ 4: Cho hàm số y = f(x) là một hàm số đa thức.
Ví dụ: Tìm tập xác định của hàm số y = x^2 + 3x – 4.
Lời giải:
Để biểu thức x^2 + 3x – 4 có nghĩa thì x^2 + 3x – 4 ≠ 0.
=> (x + 4)(x – 1) ≠ 0.
=> x ≠ -4 và x ≠ 1.
=> Tập xác định của hàm số là D = (-∞; -4) ∪ (-4; 1) ∪ (1; +∞).
Ví dụ 5: Cho hàm số y = f(x) là một hàm số chứa căn thức.
Ví dụ: Tìm tập xác định của hàm số y = √(x – 2).
Lời giải:
Để biểu thức √(x – 2) có nghĩa thì x – 2 ≥ 0.
=> x ≥ 2.
=> Tập xác định của hàm số là D = [2; +∞).
Ví dụ 6: Cho hàm số y = f(x) là một hàm số chứa logarit.
Ví dụ: Tìm tập xác định của hàm số y = log2(x + 1).
Lời giải:
Để biểu thức log2(x + 1) có nghĩa thì x + 1 > 0.
=> x > -1.
=> Tập xác định của hàm số là D = (-∞; -1) ∪ [-1; +∞).
Ví dụ 7: Cho hàm số y = f(x) là một hàm số chứa lượng giác.
Ví dụ: Tìm tập xác định của hàm số y = sin(x).
Lời giải:
Để biểu thức sin(x) có nghĩa thì x ∈ R.
=> Tập xác định của hàm số là D = R.
Ví dụ 8: Cho hàm số y = f(x) là một hàm số chứa tham số.
Ví dụ: Tìm tập xác định của hàm số y = f(x) = x^2 – m, với m là tham số.
Lời giải:
Để biểu thức x^2 – m có nghĩa thì x^2 – m ≠ 0.
=> x^2 ≠ m.
=> x ≠ √m và x ≠ -√m.
=> Tập xác định của hàm số là D = R \ {√m; -√m}.
Ngoài ra, còn có một số bài tập trắc nghiệm tìm tập xác định hàm số lớp 10 khác, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức về hàm số, tập hợp và logic toán.
Dưới đây là một số lưu ý khi giải bài tập trắc nghiệm tìm tập xác định hàm số lớp 10:
- Khi giải bài tập trắc nghiệm tìm tập xác định hàm số lớp 10, học sinh cần lưu ý phân biệt giữa tập xác định và miền giá trị của hàm số.
- Để tìm tập xác định của hàm số, học sinh cần xem xét biểu thức của hàm số và xác định xem biểu thức đó có nghĩa khi x nhận giá trị nào.
- Khi gặp bài tập trắc nghiệm tìm tập xác định hàm số chứa tham số, học sinh cần chú ý đến giá trị của tham số trong từng câu hỏi.
Bài tập tìm tập xác định của hàm số f(x)
Dưới đây là một số dạng bài tập tìm tập xác định của hàm số f(x) như sau:
Dạng 1: Hàm số đơn giản
Hãy xem xét hàm số f(x) = 2x – 3. Hỏi tập xác định của hàm số này là gì?
Lời giải: Tập xác định của hàm số f(x) = 2x – 3 là tất cả các số thực, vì bạn có thể thay bất kỳ giá trị nào cho x và tính được giá trị tương ứng của hàm số.
Dạng 2: Hàm số có biểu thức chia
Xét hàm số f(x) = 1/(x – 2). Hỏi tập xác định của hàm số này là gì?
Lời giải: Tập xác định của hàm số f(x) = 1/(x – 2) là tất cả các số thực ngoại trừ x = 2, vì chia cho 0 (x – 2 = 0) không xác định.
Dạng 3: Hàm số với căn bậc 2
Xét hàm số f(x) = √(x + 4). Hỏi tập xác định của hàm số này là gì?
Lời giải: Tập xác định của hàm số f(x) = √(x + 4) là các số thực x sao cho x + 4 phải lớn hơn hoặc bằng 0 (vì căn bậc 2 của số âm không xác định trong tập số thực). Vì vậy, tập xác định là các số thực x sao cho x >= -4.
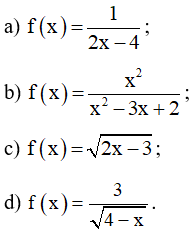
Dạng 4: Hàm số vô hướng có biểu thức bậc 2
Xét hàm số f(x) = x^2 – 6x + 9. Hỏi tập xác định của hàm số này là gì?
Lời giải: Tập xác định của hàm số f(x) = x^2 – 6x + 9 là tất cả các số thực, vì bạn có thể thay bất kỳ giá trị nào cho x và tính được giá trị tương ứng của hàm số.
Dạng 5: Hàm số kết hợp các yếu tố trên
Xét hàm số f(x) = √(4x – 1)/(3x^2 + 2). Hỏi tập xác định của hàm số này là gì?
Lời giải: Để tìm tập xác định, bạn cần xác định các giới hạn cho biểu thức bên trong căn bậc 2 và mẫu số. Trong trường hợp này, biểu thức bên trong căn bậc 2 (4x – 1) phải lớn hơn hoặc bằng 0 (vì căn bậc 2 của số âm không xác định) và mẫu số (3x^2 + 2) không được bằng 0. Sau khi giải các bất đẳng thức này, bạn sẽ có tập xác định của hàm số.
Những dạng bài tập này giúp bạn nắm vững cách xác định tập xác định của hàm số dựa trên các yếu tố cụ thể trong biểu thức hàm số.
Hy vọng các thông tin trên sẽ giúp mọi người hiểu được các cách tìm tập xác định hàm số lớp 10 chuẩn nhất. Để nắm vững kiến thức này, học sinh cần luyện tập giải các bài tập liên quan một cách thường xuyên. Cần nắm vững các kiến thức về biểu thức đại số, đặc biệt là các định lý về căn bậc hai, căn bậc ba và hãy luôn chú ý đến các dấu ngoặc trong biểu thức hàm số.