Công thức cách tính đường chéo trong hình vuông là một trong những công thức khá phổ biến trong quá trình áp dụng bài tập hình học. Để hiểu rõ hơn về nền tảng cơ bản cho những bài tập liên quan đến đường chéo hình vuông này mọi người cùng dapanchuan.com nhà tớ theo dõi bài viết ngay sau đây nhé!
Hình vuông-Lý thuyết chung
Hình vuông là gì?
Trong hình học Eculid, hình vuông được địnhnghĩa như sau: hinh vuông là một hình tứ giác đều, có bốn cạnh bằng nhau và bốn góc bằng nhau (4 góc vuông, 4 góc bằng 90 độ).
Trong lý thuyết, hình vuông là một dạng đặc biệt của hình chữ nhật và hình thơi, hình chữ nhật có các cạnh bằng nhau là hình vuông và hình thoi có hai đường chéo bằng nhau là hình vuông.
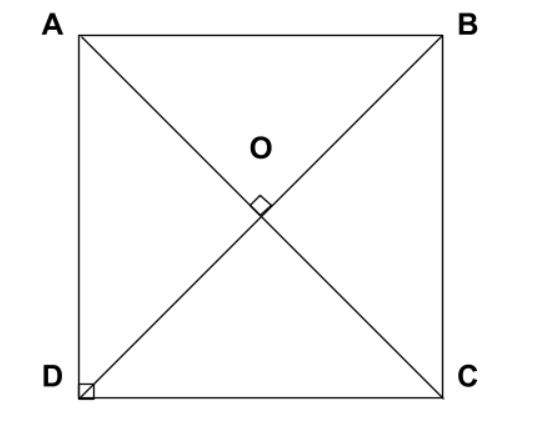
Tính chất hình vuông
Trong hình vuông, có những tính chất sau đây:
+Có hai cặp cạnh song song
+Có 4 cạnh bằng nhau
+Hai đường chéo bằng nhau, vuông góc và giao nhau tại trung điểm mỗi đường
+Có đường tròn ngoại tiếp và nội tiếp đồng thời tâm đường tròn là giao điểm của hai đường chéo hình vuông
+1 đường chéo hình vuông sẽ chia thành 2 hình có diện tích bằng nhau
+Giao điểm của các đường phân giác, trung tuyến, trung điểm đều trùng tại một điểm
+Có tất cả các hình chất của hình chữ nhật hình thang và hình thoi
Đường chéo hình vuông là gì?
Đường chéo hình vuông được định nghĩa là đường thăng nối liên hai góc vuông đối diện nhau và chia hình vuông thành hai nữa tam giác bằng nhau.
Tính chất đường chéo của hình vuông bao gôm:
+Mỗi hình vuông sẽ có hai đường chéo bằng nhau, giao nhau tại trung điểm mỗi đường và vuông góc với nhau.
+Đường chéo chia hình vuông thành hai tam giác vuông cân bằng nhau
+Giao điểm của hai đường chéo hình vuông là tâm đường tron ngoiaj tiếp và nội tiếp hình vuông đó.
Công thức cách tính đường chéo trong hình vuông
Xét hình vuông, ta có:
+2 đường chéo bằng nhau và vuông góc với nhau (tính chất hình vuông)
+Ngoài ra, đường chéo hình vuông chia thanh hai tam giác vuông cân có diện tích bằng nhau.
+Suy ra, đường chéo hình vuông lúc này là cạnh huyền của hai tam giác vuông cân đó
+Đường chéo hình vuông lúc này được suy ta từ định lý pytago:
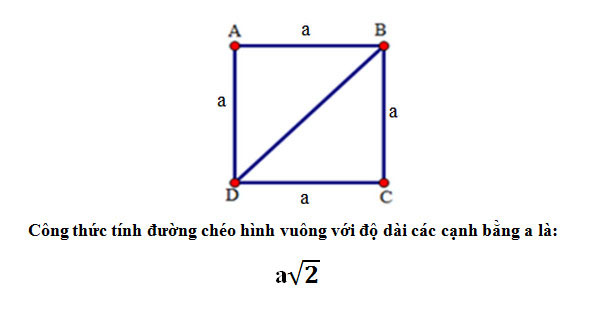
Gọi cạnh hình vuông có độ dài bằng a, đường chéo có độ dàu bằng b ta có:
- b = căn (a2+a2) = a căn 2
Bài tập: Cho hình vuông ABCD, độ dài các cạnh AB = BC = CD = DA = a, tính hình chéo BD, AC.
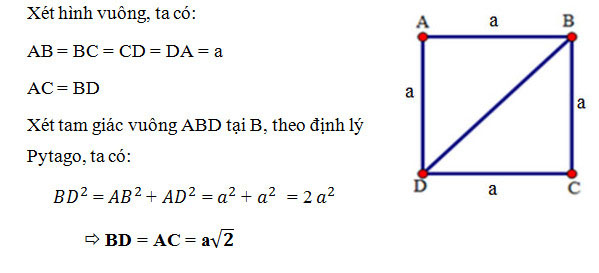
Dấu hiệu nhận biết hình vuông
Trong mỗi đề bài, đôi khi người ta sẽ không lý giải và cho sẵn một hình vuông mà phải chứng minh đó là hình vuông sau đó mói đi tìm đường chéo. Chính vì thế mà dấu hiệu nhận biết về hình vuông là một trong những kiến thức không thể thiếu, mọi người nắm kỹ kiến thức như sau:
+Hình chữ nhật có hai cạnh kề bằng nhau
+Hình chữ nhật có hai đường chéo vuông góc
+Hình chữ nhật có một đường chéo là phân giác một góc
+Hình thoi có một góc vuông
+Hình thoi có một đường chéo bằng nhau
+Hình bình hành có một góc vuông và hai cạnh kể bằng nhau
Trên đây là toàn bộ kiến thức về công thức cách tính đường chéo trong vuông dành đến bạn đọc. Mọi người cần nắm rõ công thức để áp dụng vào bài tập một cách nhanh chóng và chính xác nhật. Hi vọng các bạn sẽ thấy hình học thật dễ và thú vị hơn sau những đáp án mà nhà tớ đưa ra. Cảm ơn đã theo dõi hết bài viết!