Tính chất đường trung tuyến trong tam giác cân như sau: Trong tam giác cân, đường trung tuyến ứng với cạnh đáy vuông góc với cạnh đáy và chia tam giác thành hai tam giác nhỏ bằng nhau. Vậy thì công thức tính đường trung tuyến và cách để chứng minh đường trung tuyến ra sao, hãy cùng DapAnChuan.Com tìm hiểu cụ thể hơn ngay bên dưới!
Định nghĩa đường trung tuyến của tam giác?
Đường trung tuyến của một tam giác là đường thẳng đi qua một đỉnh của tam giác và chia đôi đoạn thẳng nối đỉnh đó với trung điểm của cạnh đối diện. Mỗi tam giác có ba đường trung tuyến, chúng tạo thành một hệ thống giao điểm tại một điểm duy nhất, gọi là trọng tâm của tam giác.
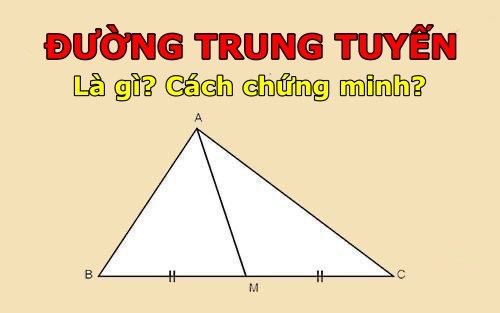
Trọng tâm là tâm của tứ giác được tạo thành bởi ba trung điểm của các cạnh của tam giác. Đường trung tuyến chứa trọng tâm và có độ dài bằng một nửa độ dài cạnh đối diện. Đường trung tuyến có tính chất đặc biệt và được sử dụng trong nhiều bài toán liên quan đến tam giác.
Tính chất đường trung tuyến trong tam giác cân
Trong tam giác cân, đường trung tuyến ứng với cạnh đáy là đoạn thẳng vuông góc với cạnh đáy và chia tam giác thành hai tam giác nhỏ bằng nhau.
Chứng minh:
Xét tam giác cân ABC có cạnh đáy là BC và đỉnh cao là A. Đường trung tuyến AM đi qua trung điểm M của cạnh BC.
- AM vuông góc với BC:
- Từ M kẻ đường vuông góc với BC tại N. Ta có MN = MB/2.
Xét tam giác MAN và tam giác CAM, ta có:
- MAN = CAM = 90o
- AM = CM = MN
- AN = CM – MN = 0
Vậy tam giác MAN và tam giác CAM là hai tam giác vuông cân bằng cạnh huyền AM. Do đó, AM vuông góc với BC.
AM chia tam giác ABC thành hai tam giác nhỏ bằng nhau:
Xét tam giác ABC và tam giác ABM, ta có:
- AB = AC
- BM = BC/2 = AC/2
- AM = CM = MN = MB/2 = AC/2
Vậy, tam giác ABC và tam giác ABM có:
- cạnh huyền AB = cạnh huyền AC
- góc ACB = góc ACB
- độ dài đường trung tuyến AM = độ dài đường trung tuyến CM
Do đó, tam giác ABC và tam giác ABM bằng nhau.
Kết luận: Trong tam giác cân, đường trung tuyến ứng với cạnh đáy là đoạn thẳng vuông góc với cạnh đáy và chia tam giác thành hai tam giác nhỏ bằng nhau.
Một số bài tập áp dụng tính chất đường trung tuyến trong tam giác cân:
- Cho tam giác ABC cân tại A, có AB = AC = 6 cm và BC = 8 cm. Tính độ dài đường trung tuyến AM.
- Cho tam giác ABC cân tại A, có AB = AC = 5 cm và BC = 10 cm. Tính độ dài đường trung tuyến AM.
- Cho tam giác ABC cân tại A, có AB = AC = x và BC = 2x. Tính độ dài đường trung tuyến AM.
- Cho tam giác ABC cân tại A, có AB = AC = 2x và BC = 3x. Tính độ dài đường trung tuyến AM.
>>> Tìm hiểu thêm: Cho hình thang cân abcd có ab//cd và ab <dc Giải toán lớp 8 chuẩn nhất
Tính chất đường trung tuyến trong tam giác vuông cân
Đường trung tuyến trong tam giác vuông cân có hai tính chất chính sau:
Đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền. Các đường trung tuyến, đường cao, đường phân giác kẻ từ đỉnh góc vuông của tam giác vuông cân trùng nhau và bằng 1 nửa cạnh huyền.
Chứng minh:
Tính chất 1
Xét tam giác vuông cân ABC tại A, với AB = AC = a. Đường trung tuyến AM của tam giác này là đường phân giác của góc A, đồng thời là đường cao của tam giác này.
Tam giác vuông cân ABC với đường trung tuyến AM
Do đó, theo định lý Pythagoras, ta có:
- AM^2 = BM^2 + MC^2
- AM^2 = (AC/2)^2 + (AC/2)^2
- AM^2 = AC^2/2 + AC^2/2
- AM^2 = AC^2
- AM = AC/2
Tính chất 2
Do đường trung tuyến AM là đường phân giác của góc A, đồng thời là đường cao của tam giác này, nên AM vuông góc với BC. Do đó, các đường trung tuyến, đường cao, đường phân giác kẻ từ đỉnh góc vuông của tam giác vuông cân trùng nhau và bằng 1 nửa cạnh huyền.
Tính chất đường trung tuyến trong tam giác vuông cân có thể được ứng dụng để giải các bài toán sau:
- Tính cạnh huyền của tam giác vuông cân khi biết đường trung tuyến ứng với cạnh huyền.
- Tính diện tích của tam giác vuông cân khi biết đường trung tuyến ứng với cạnh huyền.
- Tính độ dài của một đường trung tuyến trong tam giác vuông cân khi biết độ dài của cạnh huyền.
>>> Xem thêm: Giao điểm 3 đường cao là gì Tính chất
Tính chất đường trung tuyến trong tam giác đều
Trong tam giác đều, đường trung tuyến có các tính chất sau:
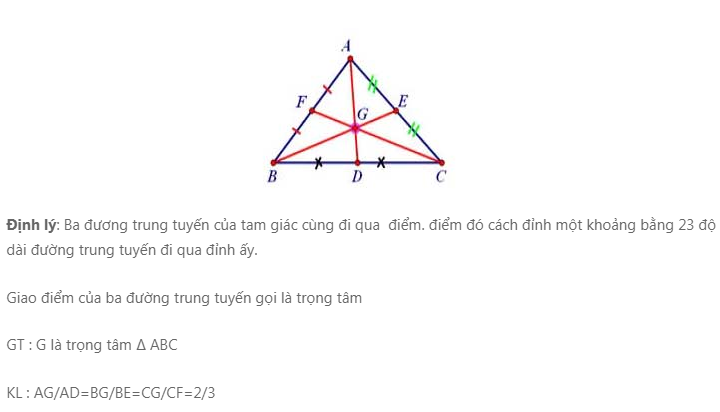
- Ba đường trung tuyến của tam giác đều cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy. Giao điểm của ba đường trung tuyến gọi là trọng tâm.
- Trong tam giác đều đường thẳng đi qua một đỉnh bất kỳ và đi qua trọng tâm của tam giác sẽ chia tam giác đó thành hai tam giác có diện tích bằng nhau.
Chứng minh: Ba đường trung tuyến của tam giác đều cùng đi qua một điểm.
Gọi ABC là tam giác đều với AB=AC=BC=a. Gọi M là trung điểm của cạnh AC.
- Xét tam giác ABC, có AM=BC/2=a/2.
- Xét tam giác AMC, có CM=AC/2=a/2.
Do đó, AM=CM.
Tương tự, ta có BM=CN.
Vậy ba đường trung tuyến AM, BM, CN cùng đi qua một điểm G.
Trong tam giác đều đường thẳng đi qua một đỉnh bất kỳ và đi qua trọng tâm của tam giác sẽ chia tam giác đó thành hai tam giác có diện tích bằng nhau.
Gọi G là trọng tâm của tam giác ABC.
- Xét tam giác ABC, có CG=a/3.
- Xét tam giác AGC, có GC=a/3.
Do đó, AG=AC−GC=a−a/3=2a/3.
Tương tự, ta có BG=BC−GC=2a/3.
Vậy tam giác AGC và tam giác BGC có diện tích bằng nhau.
>>> Xem thêm: Khi nào có bằng tốt nghiệp thpt chính thức sau khi thi
Định lý đường trung tuyến trong tam giác cân
Định lý 1: Trong tam giác cân, đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đáy và chia tam giác thành hai tam giác bằng nhau.
Chứng minh:
- Xét tam giác cân ABC có AB = AC.
- Nối A với trung điểm D của BC.
Ta có:
- AD là đường trung tuyến của tam giác ABC.
- AD là phân giác của góc A.
- AD là đường cao của tam giác ABD.
- Do đó, AD vuông góc với BC.
Mặt khác, AD là phân giác của góc A nên:
- AB/AC = AD/DC
- Do AB = AC nên AD = DC.
Do đó, tam giác ABD và tam giác ADC là hai tam giác bằng nhau.
Định lý 2: Trong tam giác cân, đường trung tuyến ứng với cạnh đáy thì chia tam giác thành hai tam giác có diện tích bằng nhau.
Chứng minh:
- Xét tam giác cân ABC có AB = AC.
- Nối A với trung điểm D của BC.
Ta có:
- Tam giác ABD và tam giác ADC là hai tam giác bằng nhau.
- Diện tích tam giác = (1/2)bh.
Do đó, diện tích tam giác ABD = diện tích tam giác ADC.
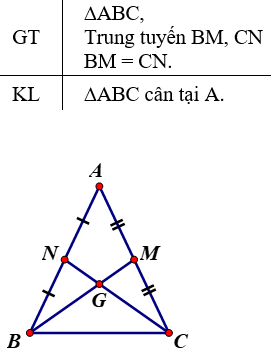
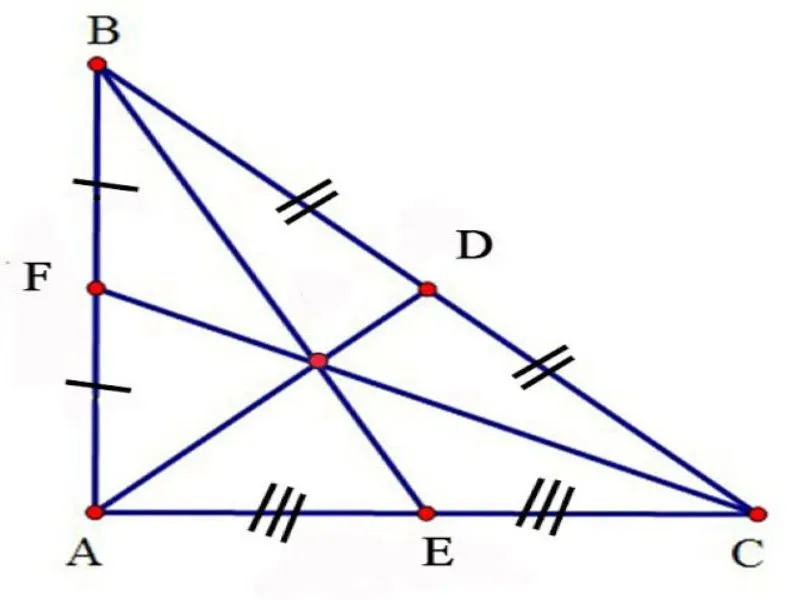
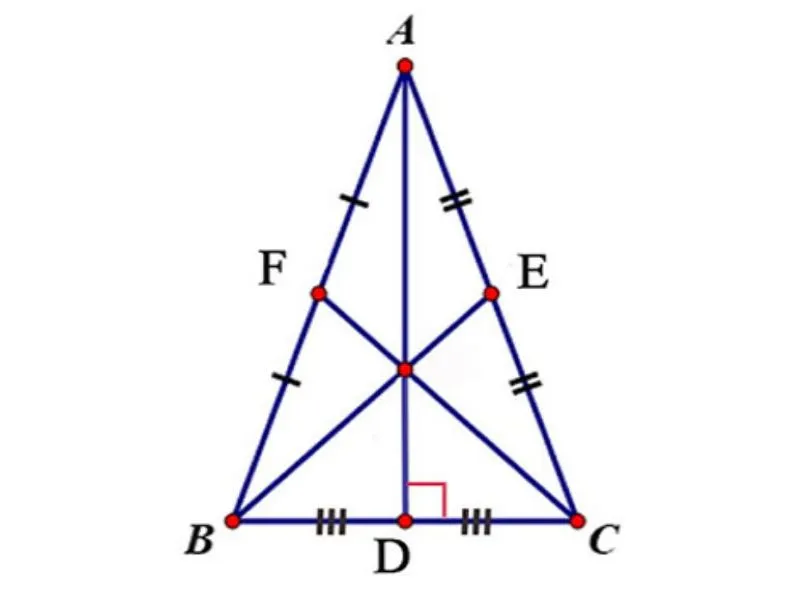
Định lý 3: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
Chứng minh:
- Xét tam giác ABC.
- Nối A với trung điểm D của BC.
- Nối B với trung điểm E của AC.
- Nối C với trung điểm F của AB.
Ta có:
- AD là đường trung tuyến của tam giác ABC.
- BE là đường trung tuyến của tam giác BAC.
- CF là đường trung tuyến của tam giác ABC.
- Do đó, AD, BE và CF cùng đi qua một điểm O.
Mặt khác,
- AO = 2/3 AD
- BO = 2/3 BE
- CO = 2/3 CF
Do đó, O cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
Tổng kết:
- Trong tam giác cân, đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đáy và chia tam giác thành hai tam giác bằng nhau.
- Trong tam giác cân, đường trung tuyến ứng với cạnh đáy thì chia tam giác thành hai tam giác có diện tích bằng nhau.
- Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
>>> Tìm hiểu thêm: Cách Tính đường cao trong tam giác cân
Công thức tính độ dài đường trung tuyến trong tam giác cân
Trong tam giác cân, đường trung tuyến chia tam giác thành hai tam giác nhỏ bằng nhau. Do đó, độ dài đường trung tuyến của tam giác cân bằng nửa độ dài cạnh đáy.
Công thức tính độ dài đường trung tuyến trong tam giác cân là:
d = (1/2) * a
Trong đó:
- d là độ dài đường trung tuyến
- a là độ dài cạnh đáy
Ví dụ: Cho tam giác cân ABC có cạnh đáy AB = 10 cm. Tính độ dài đường trung tuyến AM.
d = (1/2) * AB = (1/2) * 10 = 5 cm
Như vậy, độ dài đường trung tuyến AM là 5 cm.
Lưu ý: Công thức trên chỉ áp dụng cho tam giác cân. Đối với tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền. Đối với tam giác thường, độ dài đường trung tuyến có thể được tính bằng cách sử dụng định lý Pythagore.
Công thức đường trung tuyến trong tam giác đều cạnh a
Trong tam giác đều, các cạnh có độ dài bằng nhau, do đó đường trung tuyến cũng có độ dài bằng nhau. Công thức tính đường trung tuyến trong tam giác đều cạnh a là:
d = a/2
Trong đó:
- d là độ dài đường trung tuyến
- a là độ dài cạnh của tam giác đều
Ví dụ: Cho tam giác đều ABC có cạnh a = 5 cm. Độ dài đường trung tuyến AM là:
AM = a/2 = 5/2 = 2,5 cm
Lưu ý: Công thức tính đường trung tuyến trong tam giác đều chỉ áp dụng cho tam giác đều. Đối với các loại tam giác khác, công thức tính đường trung tuyến sẽ khác.
Cách chứng minh đường trung tuyến trong tam giác cân
Để chứng minh đường trung tuyến trong tam giác cân, ta có thể sử dụng các cách sau:
Cách 1:
Cho tam giác cân ABC với AB = AC, và đường trung tuyến AM.
Gọi E là trung điểm của cạnh BC.
Ta có:
- AE = EC
- AM = CM
Từ đó, ta có tam giác AME cân tại E.
- Do đó, AE = ME.
- Nhưng ME = AC/2.
- Suy ra, AM = AC/2.
Cách 2:
Cho tam giác cân ABC với AB = AC, và đường trung tuyến AM.
Dựng đường cao BE từ đỉnh B xuống cạnh AC.
Ta có:
- BE = BC/2
- AM = CM
Do đó, tam giác AME cân tại E.
- Do đó, AE = ME.
- Nhưng ME = AC/2 – BE = AC/2 – BC/2 = AB/2.
- Suy ra, AM = AC/2.
Cách 3:
Cho tam giác cân ABC với AB = AC, và đường trung tuyến AM.
Gọi D là trung điểm của cạnh AB.
Ta có:
- AD = AB/2 = AC/2
- DM = MC
Do đó, tam giác AMD cân tại D.
- Do đó, MD = AM.
- Suy ra, AM = AC/2.
Từ các cách chứng minh trên, ta có kết luận:
Trong tam giác cân, đường trung tuyến từ đỉnh đến cạnh đáy là đoạn thẳng vuông góc với cạnh đáy và chia tam giác thành hai tam giác nhỏ bằng nhau.
Bài tập về đường trung tuyến trong tam giác cân, vuông cân
Dưới đây là một số bài tập về đường trung tuyến trong tam giác cân, vuông cân:
Bài 1:
Cho tam giác cân ABC có AB = AC = 6 cm và BC = 8 cm. Tính độ dài đường trung tuyến AM.
Giải:
- Ta có: AM = AC/2 = 6/2 = 3 cm.
- Đáp án: 3 cm.
Bài 2:
Cho tam giác vuông cân ABC có AB = AC = 8 cm. Tính độ dài đường trung tuyến AM.
Giải:
- Ta có: AM = AC/2 = 8/2 = 4 cm.
- Đáp án: 4 cm.
Bài 3:
Cho tam giác cân ABC có AB = AC = 13 cm. Gọi M là trung điểm của cạnh BC. Tính diện tích tam giác AMC.
Giải:
Ta có: S_AMC = 1/2 * AM * MC
= 1/2 * 13/2 * 13/2
= 91/4
Đáp án: 91/4 cm^2.
Bài 4:
Cho tam giác vuông cân ABC có AB = AC = 12 cm. Gọi M là trung điểm của cạnh BC. Tính khoảng cách từ điểm M đến cạnh AB.
Giải:
Ta có: BM = MC = 12/2 = 6 cm
AM^2 = BM^2 + MC^2
= 6^2 + 6^2
= 72
AM = √72 = 6√2
Đáp án: 6√2 cm.
Ngoài ra, còn rất nhiều bài tập về đường trung tuyến trong tam giác cân, vuông cân. Để giải được các bài tập này, ta cần nắm vững các tính chất của đường trung tuyến trong tam giác.
Hy vọng các thông tin bên trên sẽ giúp mọi người nắm rõ được tính chất đường trung tuyến trong tam giác cân, vuông cân từ đó có thể hiểu rõ về các tính chất về đường trung tuyến.Hãy vận dụng kiến thức này để giải quyết các bài toán một cách hiệu quả. Mong rằng bài viết trên sẽ giúp bạn nắm vững các tính chất này và giải được các bài tập liên quan một cách dễ dàng.