Xác định phần ảo của số phức, số phức thuần ảo

Khi học trung học phổ thông thì phần số phức luôn khiến các bạn học sinh đau đầu. Mà đăc biệt là việc phải xác định phần ảo của số phức, số phức thuần ảo. Vì thế với bài viết ngày hôm nay chúng tôi sẽ giúp bạn phân biệt rõ hơn về 2 phần này trong số phức nhé.

Vậy số phức là gì?

Số phức là số có thể viết dưới dạng $a+b\imath$ , trong đó a và b là các số thực (số nguyên), a được gọi là phần thực, b được gọi là phần ảo. Và $\imath$ được xem là đơn vị ảo, qui ước $\imath ^{2}=-1$ hay $\imath ={\sqrt {-1}}$ (Ví dụ : $-3,5+2\imath$ là một số phức)

Phần thực và phần ảo của số Phức, số phức thuần ảo

Tập hợp số phức được kí hiệu là C. Nếu z là số thực thì phần ảo b = 0, ngược lại, nếu z là số thuần ảo thì phần thực của z là a = 0. (Số phức thuần ảo là số phức có phần thực bằng 0).

Mỗi số thực $a$ được xem là một số phức có b=0.

Ta có: $\mathbb {R}$ $\subset$ $\mathbb{C}$

Nếu a=0, số phức $bi$ được gọi là thuần ảo.

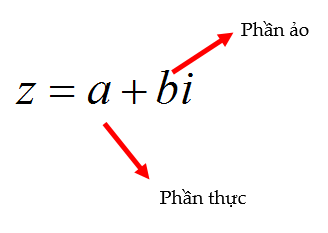
Mỗi số phức z đều được biểu diễn duy nhất dưới dạng: $z=a+bi$ . Trong đó a, b là các số thực. Dạng biểu diễn này được gọi là dạng đại số của số phức z.

Bài tập mẫu về số phức thuần ảo

ĐỀ BÀI: Số phức nào dưới đây là số thuần ảo?

A. z = -2 + 5 $\imath$
B. z = 5 $\imath$
C. z = -2
D. z = √5 + $\imath$

BÀI GIẢI

Số ảo là $z=a+bi$ .

Nếu a=0, số phức $bi$ được gọi là thuần ảo.

Thỏa điều kiện trên: là đáp án B. z = 5 $\imath$

Hi vọng với bài viết Xác định phần ảo của số phức, số phức thuần ảo và bài tập ví dụ mà chúng tôi mang đến đã phần nào giúp bạn xác định được đâu là phần thực và đâu là phần ảo cũng như số phức thuần ảo là như thế nào nhé. Chúc các bạn học tập tiến bộ hơn trong tương lai. Mặc dù các kiến thức trên internet cũng rất hữu ích nhưng các bạn cũng nên tham khảo ý kiến của giáo viên bộ môn của các bạn nhé.

Viết một bình luận Hủy