Phương pháp nhân 2 số phức, số phức nhân số phức liên hợp là một trong những bài tập khiến khá nhiều các bạn học sinh quan tâm và lo lắng khi gặp những bài tập dạng như thế này. Vì thế với bài viết ngày hôm nay, Dapanchuan.com sẽ giuspo bạn giải đáp vấn đè này một cách chi tiết nhất để các bạn có thể cũng cố lại kiến thứ nền về số phức và số phức liên hợp.

Vậy số phức là gì?
Số phức là số có thể viết dưới dạng 




Tập hợp số phức được kí hiệu là C. Nếu z là số thực thì phần ảo b = 0, ngược lại, nếu z là số thuần ảo thì phần thực của z là a = 0.
Mỗi số phức z đều được biểu diễn duy nhất dưới dạng: 
Biểu diễn hình học của số phức:
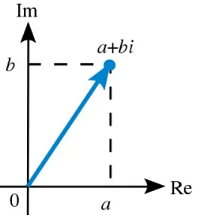
Cho số phức z = a + bi (a,b nguyên). Xét trong mặt phẳng phức Oxy, z sẽ được biểu diễn bởi điểm M(a;b) hoặc bởi vector u = (a;b).
Chú ý ở mặt phẳng phức, trục Ox còn được gọi là trục thực, trục Oy gọi là trục ảo.
Số phức liên hợp là gì?
Có thể thấy, số phức liên hợp là gì là câu hỏi được nhiều bạn học sinh khá quan tâm. Dưới đây là những kiến thức cụ thể về số phức liên hợp là gì.
Như đã biết, số phức là một biểu thức có dạng 



Một số tính chất của số phức liên hợp:




Phương pháp nhân 2 số phức
Số phức có dạn 

Công thức nhân hai số phức:
Trong trường số phức, tính chất của đơn vị ảo 
Mỗi số phức z đều được biểu diễn duy nhất dưới dạng: 
Với cách biểu diễn dưới dạng đại số, phép cộng và nhân các số phức được thực hiện như phép cộng và nhân
các nhị bất đẳng thức với lưu ý rằng i2 = –1. Như vậy, ta có:
Số phức nhân số phức liên hợp
Như đã biết, số phức là một biểu thức có dạng 



Một số tính chất của số phức liên hợp:




Module và Argument của số phức:
Cho 




Có thể biểu diễn số phức 






Một vài tính chất của module và argument
Dạng lượng giác của số phức:
Số phức 
Khi đặt : 
Ta có:
Cách biểu diễn này được gọi là dạng lượng giác của số phức 
Phép toán trên các số phức viết dưới dạng lượng giác
Phép nhân và phép chia các số phức dưới dạng lượng giác
Cho hai số phức dưới dạng lượng giác
Khi đó:
Lũy thừa tự nhiên của số phức dưới dạng lượng giác (công thức Moirve).
Khai căn số phức dưới dạng lượng giác.
Mọi số phức z khác 0 đều có đúng n căn bậc n, là các số dạng
trong đó 
Hi vọng với bài viết Phương pháp nhân 2 số phức, số phức nhân số phức liên hợp sẽ giúp bạn có thêm thật nhiều kiến thức để phục vụ trong học tập nhé.
















![{\displaystyle {\omega }_{k}={\sqrt[{n}]{r}}\left(\cos {\psi }_{k}+i\sin {\psi }_{k}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a03dd7d07b639e386d3e187aac1866ee12ba466b)
