Như các em học sinh đã biết, liên quan đến dạng bài về tam giác thì sẽ không thể nào thiếu dạng hai tam giác bằng nhau. Các trường hợp bằng nhau của hai tam giác vuông cũng khá phổ biến và thường gặp trong quá trình học bộ môn toán của các em. Vậy nên, DapAnChuan.com có mặt ở đây và sẽ giúp các học sinh nắm rõ về các trường hợp này, qua nội dung bài viết sau đây, mọi người cùng tham khảo
Thế nào là hai tam giác bằng nhau?
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Hai tam giác được gọi là “bằng nhau” (hoặc “đồng dạng”) khi chúng có cùng diện tích và cùng dạng. Điều này có nghĩa là tổng các độ dài các cạnh tương ứng của hai tam giác phải bằng nhau và góc tương ứng của chúng cũng phải bằng nhau.
Để hai tam giác được coi là bằng nhau, chúng phải thỏa mãn một trong các điều kiện sau:
- Hai cạnh và một góc giống nhau: Hai cạnh của một tam giác và một góc giữa chúng giống với hai cạnh và góc tương ứng của tam giác kia.
- Ba cặp cạnh giống nhau: Ba cặp cạnh tương ứng của hai tam giác phải có độ dài bằng nhau.
Các trường hợp bằng nhau của tam giác vuông
Đối với tam giác vuông, hai tam giác được gọi là bằng nhau nếu có sự tương đồng hoàn toàn giữa chúng, đồng nghĩa với việc các cặp cạnh và góc tương ứng của hai tam giác đều bằng nhau. Cụ thể, các trường hợp sau phải được thoả mãn:
Hai cạnh góc vuông (cạnh – góc – cạnh)
Định nghĩa
Nếu hai tam giác vuông có cạnh góc vuông của mỗi tam giác lần lượt bằng nhau, tức là cạnh góc vuông của tam giác vuông thứ nhất có độ dài bằng cạnh góc vuông của tam giác vuông thứ hai, thì hai tam giác này được gọi là bằng nhau
Theo như hình trên:
– Cạnh AB = cạnh DE
– Cạnh AC = cạnh DF
=> Theo trường hợp 1 thì hai tam giác ABC (vuông tại A) và tam giác DEF (vuông tại D) bằng nhau
Cạnh góc vuông và góc nhọn kề cạnh đó (góc – cạnh – góc)
Nếu chúng ta xem xét hai tam giác vuông khác nhau, mỗi tam giác có một cạnh góc vuông và một góc nhọn kề cạnh góc vuông đó, và các góc này bằng nhau, thì điều này dẫn đến một kết luận quan trọng: hai tam giác vuông đó hoàn toàn bằng nhau.
Để giải thích điều này một cách chi tiết hơn, hãy xem xét hai tam giác vuông, gọi chúng lần lượt là tam giác ABC và tam giác XYZ. Trong tam giác ABC, chúng ta có một cạnh góc vuông AB và một góc nhọn kề cạnh AB. Tương tự, trong tam giác XYZ, chúng ta có một cạnh góc vuông XZ và một góc nhọn kề cạnh XZ.
Nếu chúng ta biết rằng góc ABC và góc XYZ bằng nhau, tức là ABC = XYZ và AB = XZ (vì chúng ta đã cho rằng các cạnh góc vuông là bằng nhau), thì theo nguyên tắc của tam giác, hai tam giác này bằng nhau. Chúng ta có thể sử dụng nguyên tắc tương tự để chứng minh bằng nhau của các cặp góc và cạnh khác trong hai tam giác.
Như vậy, kết luận là nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia, thì hai tam giác vuông đó hoàn toàn bằng nhau.
Hình 1
Ở hình trên ta thấy:
– Góc A và góc D đều vuông ( bằng 90 độ )
– Cạnh AC = cạnh DF
– Góc C bằng góc F
=> Ta nói tam giác ABC (vuông tại A) bằng tam giác DEF (vuông tại D)
Cạnh huyền – góc nhọn (góc – cạnh -góc)
Khi hai tam giác vuông có cạnh huyền và một góc nhọn tương đồng, ta có một trường hợp tương đồng tam giác, trong đó các cạnh tương ứng của hai tam giác có độ dài bằng nhau.
Hai tam giác vuông được xem là bằng nhau nếu các cạnh của chúng tương ứng theo thứ tự giống nhau. Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia, thì ta có sự tương đồng về các cạnh và góc, và do đó, hai tam giác vuông đó là tam giác bằng nhau (có cùng hình dạng và kích thước).
Ta nhìn lên Hình 1
Nếu trong tam giác vuông ABC (vuông tại A) và tam giác vuông DEF (vuông tại D) có:
– Cạnh BC = cạnh EF
– Góc C = góc F (hoặc góc B bằng góc E)
Thì hai tam giác vuông này bằng nhau.
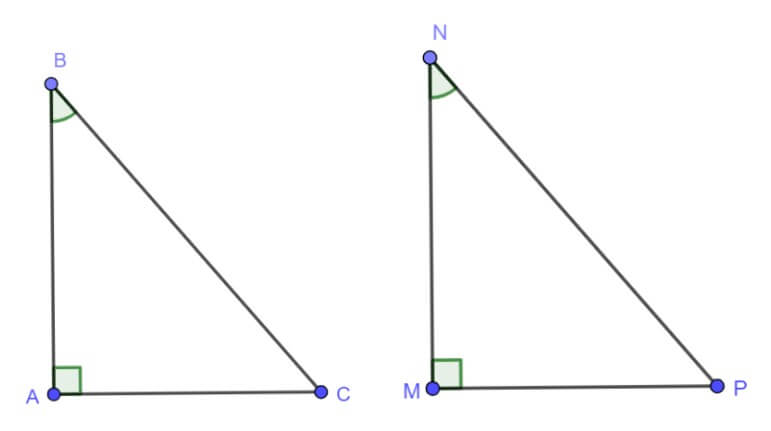
Cạnh huyền – Cạnh góc vuông
Định nghĩa: Khi nói rằng hai tam giác vuông bằng nhau, ta đang xét đến việc chúng có các góc tương ứng và các cạnh tương ứng bằng nhau. Điều này xảy ra khi cạnh huyền và một cạnh góc vuông của một tam giác vuông bằng với cạnh huyền và một cạnh góc vuông của tam giác vuông khác.
Tương tự cũng lấy ví dụ Hình 1 bên trên
Nếu trong tam giác vuông ABC (vuông tại A) và tam giác vuông DEF (vuông tại D) có:
– Cạnh BC = cạnh EF
– Cạnh AC = cạnh DF (hoặc cạnh AB = cạnh DE)
Thì hai tam giác vuông này bằng nhau.
Các dạng bài tập về trường hợp bằng nhau của tam giác vuông
Sau đây là các dạng bài tập về trường hợp bằng nhau của tam giác vuông, các em cần tham khảo để vận dụng khi làm bài tập chứng minh 2 tam giác vuông bằng nhau
Chứng minh các tam giác vuông bằng nhau
Trong dạng này, sẽ tập trung vào việc xem xét hai tam giác vuông và kiểm tra các điều kiện để xác định xem chúng có bằng nhau hay không. Cụ thể, chúng ta sẽ xem xét bốn trường hợp: cạnh – góc – cạnh, góc – cạnh – góc, cạnh huyền – góc nhọn, và cạnh huyền – cạnh góc vuông.
- Trường hợp cạnh – góc – cạnh: Nếu hai tam giác có ba cạnh tương ứng bằng nhau và một góc tương ứng bằng nhau, thì hai tam giác đó là nhau.
- Trường hợp góc – cạnh – góc: Nếu hai tam giác có hai góc tương ứng bằng nhau và một cạnh tương ứng bằng nhau, thì hai tam giác đó là nhau.
- Trường hợp cạnh huyền – góc nhọn: Nếu hai tam giác có cạnh huyền và một góc nhọn tương ứng bằng nhau, thì hai tam giác đó là nhau.
- Trường hợp cạnh huyền – cạnh góc vuông: Nếu hai tam giác có cạnh huyền và một cạnh góc vuông tương ứng bằng nhau, thì hai tam giác đó là nhau.
Dựa vào các trường hợp trên, các em kiểm tra và so sánh các yếu tố của hai tam giác vuông để xác định xem chúng có bằng nhau theo trường hợp nào. Sau đó, đưa ra kết luận về tính bằng nhau của hai tam giác.
Chứng minh góc và đoạn thẳng bằng nhau
Bài toán này tập trung vào việc chứng minh hai tam giác bằng nhau bằng cách sử dụng kiến thức về các trường hợp bằng nhau của hai tam giác vuông. Để chứng minh sự bằng nhau của hai tam giác, chúng ta cần tìm hiểu các điều kiện và cách áp dụng chúng.
Các trường hợp bằng nhau của hai tam giác vuông:
- Nếu hai tam giác vuông có cạnh chung và góc vuông chung, chúng bằng nhau.
- Nếu một cạnh và cạnh huyền của một tam giác vuông bằng tương ứng với một tam giác vuông khác, thì hai tam giác đó bằng nhau.
Áp dụng kiến thức để chứng minh hai tam giác bằng nhau:
+ Bước 1: Xác định hai tam giác cần chứng minh bằng nhau và tìm các thông tin về chúng.
+ Bước 2: Tìm các đặc điểm chung giữa hai tam giác, ví dụ như cạnh chung, góc chung.
+ Bước 3: Kiểm tra xem hai tam giác có thoả mãn các điều kiện bằng nhau đã nêu trên hay không. Nếu có, ta có thể kết luận rằng hai tam giác đó là bằng nhau và các đoạn thẳng và góc tương ứng cũng bằng nhau.
Bài tập về các trường hợp bằng nhau của tam giác vuông có lời giải
Bài 1: Cho tam giác ABC và tam giác DEF có: ∠B = ∠E = 90°, AC = DF, ∠A = ∠F. Phát biểu nào sau đây đúng?
A. ΔABC = ΔFED
B. ΔABC = ΔFDE
C. ΔBAC = ΔFED
D. ΔABC = ΔDEF
Bài 2:
Cho tam giác ABC và tam giác KHI có: ∠A = ∠K = 90°, AB = KH, BC = HI. Phát biểu nào sau đây đúng?
A. ΔABC = ΔKHI
B. ΔABC = ΔHKI
C. ΔABC = ΔKIH
D. ΔACB = ΔKHI
Bài 3:
Cho tam giác ABC và tam giác NPM có BC = PM, ∠B = ∠P = 90° . Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh huyền – cạnh góc vuông?
A. BA = PM B. BA = PN C. CA = MN D. ∠A = ∠N
Bài 4:
Cho tam giác ABC và tam giác MNP có ∠A = ∠M = 90°, ∠C = ∠P. Cần điều kiện gì để hai tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề?
A. AC = MP B. AB = MN C. BC = NP D. AC = MN
Bài 5:
Cho góc nhọn xOy với Ot là tia phân giác. Trên Ot lấy điểm I, từ I kẻ IA ⊥ Ox tại A, tia AI cắt Oy tại N, kẻ IB ⊥ Oy tại B, tia BI cắt Ox tại M. Khi đó ta có:
A. IA = IB
B. OA = OB
C. IM = IN
D. Cả A, B, C đều đúng
Bài 6:
Cho tam giác ABC đều. Từ A kẻ AF ⊥ BC tại F, từ B kẻ BG ⊥ AC tại G. Qua C kẻ đường thẳng song song với BG cắt AF tại H. Khi đó tam giác HBC là:
A. Tam giác đều
B. Tam giác vuông
C. Tam giác vuông cân
D. Tam giác cân
Bài 7:
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (hình 147). Chứng minh rằng ΔAHB =ΔAHC (giải bằng 2 cách)
Bài 8:
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh rằng
a) HB = HC
Bài 9:
Cho ΔABC cân ở A. Vẽ BH vuông góc với AC, CK vuông góc với AB.
a) CMR AH = HK
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của góc A
Bài 10:
Cho tam giác ABC cân tại A, kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A?
Bài 11:
Cho tam giác ABC cân tại A, kẻ BH ⊥ AC, CK ⊥ AB. Gọi I là giao điểm của BH và CK. Chứng minh AI là tia phân giác của góc A.
Bài 12:
Cho tam giác ABC và tam giác DEF có . Biết AB = 9cm, AB = 12cm. Độ dài EF là:
A. 12 cm
B. 9 cm
C. 15 cm
D. 13 cm
Bài 13:
Các tam giác vuông ABC và DEF có góc A = góc D = 90o, AC = DF. Hãy bổ sung thêm một điều kiện bằng nhau để ΔABC = ΔDEF.
LỜI GIẢI – ĐÁP ÁN
Bài 1: Xét tam giác ABC vuông tại B (góc B = 90 độ) và tam giác FED vuông tại E (góc E = 90 độ) có:
-AC=DF
-Góc A = góc F
=> Tam giác ABC bằng tam giác FED (cạnh huyền – góc nhọn)
Chọn đáp án A
Bài 2:
Xét tam giác ABC và tam giác KHI có:
∠A = ∠K = 90°, AB = KH, BC = HI
⇒ ΔABC = ΔKHI (cạnh huyền – cạnh góc vuông)
Chọn đáp án A
Bài 3:
Ta có hai tam giác ABC và tam giác NPM có BC = PM, ∠B = ∠P = 90° mà BC, PM là hai cạnh góc vuông của tam giác ABC và NPM nên để hai tam giác bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông thì ta cần thêm điều kiện CA = MN
Chọn đáp án C.
Bài 4:
Ta có: ∠C = ∠P mà góc C và góc P là hai góc nhọn kề của tam giác ABC và tam giác MNP
Do đó để tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề thì cần thêm điều kiện AC = MP
Chọn đáp án A.
Bài 5:
– Xét tam giác AIO vuông tại A và tam giác BIO vuông tại B có:
+ OI: cạnh huyền chung
+ Góc O1 bằng góc O2 (Ot là tia phân giác của góc xOy)
=> Tam giác AIO = tam giác BIO (cạnh huyền – góc nhọn)
=> OA=OB; IA=IB (hai cạnh tương ứng)
– Xét tam giác IAM vuông tại A và tam giác IBN vuông tại B có:
+ IA = IB (chứng minh trên)
+ Góc AIM bằng góc BIN (hai góc đối đỉnh)
=> Tam giác IAM bằng tam giắc BIN (cạnh góc vuông – góc nhọn)
=> IM=IN (hai cạnh tương ứng)
Vậy cả A, B, C đều đúng
Chọn đáp án D
Bài 6:
+ Xét tam giác ABF và tam giác ACF đều vuông tại F có:
AB = AC (tam giác ABC đều)
AF: cạnh chung
Do đó: ΔABF = ΔACF (cạnh huyền – cạnh góc vuông)
Suy ra: BF = CF (hai cạnh tương ứng)
+ Xét hai tam giác BFH và CFH cùng vuông tại F có:
FH cạnh chung
BF = CF (cmt)
Do đó: ΔBFH = ΔCFH (hai cạnh góc vuông)
Suy ra: CH = BH (hai cạnh tương ứng)
⇒ ΔHBC cân tại H
– Ta có:
+ Góc BCG = góc GBC = 90 độ (tam giác BCG vuông tại G)
mà góc BCG = góc BCA = 60 độ (tam giác ABC đều)
nên góc GBC = 90 độ – góc BCG = 90 – 60 = 30 độ
– Lại có:
BG song song CH (giả thiết)
=> góc HCB = góc GBC = 30 độ (so le trong)
tam giác HBC cân tại H có góc ở đáy HCB bằng 30 độ
Nên ΔHBC không thể là tam giác vuông cân và tam giác đều.
Vậy A, B, C sai, D đúng
Chọn đáp án D
Bài 7:
Cách 1: Tam giác ABC cân tại A nên góc B = góc C và AB = AC
Hai tam giác vuông AHB và AHC có
AB = AC (GT)
∠B = ∠C (GT)
⇒ ΔAHB =ΔAHC (cạnh huyền – góc nhọn)
Cách 2:
Hai tam giác vuông AHB và AHC có
AB = AC (GT)
AH chung
⇒ ΔAHB = ΔAHC (cạnh huyền – cạnh góc vuông)
Bài 8:
a) Xét hai tam giác vuông ΔABH và ΔACH có:
AB = AC (gt)
AH cạnh chung
Nên ΔABH = ΔACH (cạnh huyền – cạnh góc vuông)
Suy ra HB = HC
b) Ta có ΔABH = ΔACH (cmt)
Bài 9:
a) Xét ΔABH và ΔACK có:
AB = AC (gt)
+Góc A chung
+Góc AHB = góc AKC = 90 độ
Nên Δ ABH = Δ ACK (cạnh huyền – góc nhọn).
b) Hai tam giác vuông AIK và AIH có
AH = AK (gt)
AI chung
Góc AKI và góc AHI = 90 độ
=> tam giác AIK bằng tam giác AIH (cạnh huyền – cạnh góc vuông)
=> Góc IAK = góc IAH
Vậy AI là tia phân giác của góc A.
Bài 10:
Xét hai tam giác vuông ADB và ADC đều vuông tại D có
AD chung
AB = AC (tam giác ABC cân tại A)
Nên ΔADB = ΔADC (cạnh huyền – cạnh góc vuông)
Suy ra ∠BAD = ∠CAD (góc tương ứng bằng nhau)
Mà tia AD nằm giữa tia AB và AC
Vậy AD là tia phân giác của góc BAC.
Bài 11:
Xét hai tam giác AHB vuông tại H và AKC vuông tại K có:
AB = AC (tam giác ABC cân tại A)
chung
Nên ΔAHB = ΔAKC (cạnh huyền – góc nhọn)
Suy ra AH = AK (cạnh tương ứng)
Xét tam giác AHI vuông tại H và AKI vuông tại K ta có:
AI là cạnh chung
AH = AK
Nên ΔAHI = ΔAKI (cạnh huyền – cạnh góc vuông)
⇒ ∠A1 = ∠A2 (góc tương ứng bằng nhau)
Do đó AI là tia phân giác góc A
Bài 12:
Áp dụng định lí Pytago vào tam giác vuông ABC, ta có:
BC^2=AB^2+AC^2
=> BC^2=9^2+12^2=225
=> BC = 15 (cm)
Xét tam giác ABC và tam giác DEF có:
+ AB=DE
+ Góc B = góc E
+ Góc A = góc D = 90 độ
⇒ ∆ABC = DEF (cạnh góc vuông – góc nhọn kề)
⇒ BC = EF = 15cm (hai cạnh tương ứng)
Bài 13:
+ Bổ sung AB =DE thì ΔABC = ΔDEF (cạnh – góc – cạnh)
+ Bổ sung góc C = góc F thì ΔABC = ΔDEF (góc – cạnh – góc)
+ Bổ sung BC = EF thì ΔABC = ΔDEF (cạnh huyền – cạnh góc vuông)
Bài tập tổng hợp
Bài tập lý thuyết
Bài 1: Nêu khái niệm hai tam giác bằng nhau? Vẽ hình minh?
Bài 2: Hãy nêu các trường hợp bằng nhau của tam giác vuông? Vẽ hình ảnh minh họa cho từng trường hợp?
Bài 3: Phát biểu định lí hai đường thẳng cùng vuông góc với một đường thẳng? Nêu giả thiết, kết luận? Vẽ hình minh họa.
Bài 4: Phát biểu định lí hai đường thẳng cùng vuông góc với một đường thẳng? Ghi giả thiết kết luận? Vẽ hình minh họa?
Bài 5: Phát biểu định lí ba đường thẳng song song? Ghi giả thiết kết luận? Vẽ hình minh?
Bài 6: Các em tự tìm hiểu những t/c, định lí nào có liêu quan đến các trường hợp bằng nhau của tam giác? Kể tên?
Bài tập thực hành
Bài 1: Cho tam giác ABC, kẻ BE và CD lần lượt là đường cao vuông góc với các cạnh AC, AB. Chứng minh rằng hai tam giác BCD và CBE bằng nhau, biết BD = EC.
Bài 2: Cho tam giác ACD cân tại A. Từ đỉnh A kẻ AH vuông góc với CD, H thuộc CD. Chứng minh rằng: HB = HC và AH là tia phân giác của góc BAC.
Bài 3: Cho tam giác ABC và tam giác DEF biết góc A = góc D = 90°, góc C = góc F. Cần bổ sung thêm điều kiện gì để hai tam giác ABC và tam giác DEF bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề?
A. AC = DF B. AB = DE C. BC = EF D. AC = DE
Bài 4: Cho tam giác ABC và tam giác DEF có góc B và góc E bằng nhau và bằng 90°, AC = DF, góc A = góc F. Hãy tìm phát biểu đúng trong những phát biểu sau đây?
A. ΔABC = ΔFED B. ΔABC = ΔFDE C. ΔBAC = ΔFED D. ΔABC = ΔDEF
Bài 5: Cho hai tam giác ABC và DEF lần lượt vuông tại A và D, biết AB = DE.
a) Để hai tam giác trên có thể bằng nhau theo trường hợp cạnh góc vuông và góc nhọn kề thì cần thêm điều kiện gì?
b) Để hai tam giác trên có thể bằng nhau theo trường hợp cạnh huyền và góc nhọn kề thì cần thêm điều kiện gì?
Hy vọng qua nội dung bài viết trên, các học sinh đã tiếp nhận và hiểu sâu hơn về các trường hợp bằng nhau của tam giác vuông và đã bắt đầu áp dụng quy tắc này vào bài làm. Tuy nhiên, để nâng cao trình độ và khắc phục các khó khăn, chúng ta cần tập trung vào việc luyện tập và rèn kỹ năng một cách chăm chỉ và kiên trì.