Trong hình học, đường trung tuyến là một khái niệm cơ bản và quan trọng. Đường trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác đều có ba trung tuyến. Vậy hãy cùng DapAnChuan.Com tìm hiểu cụ thể hơn về tính chất, công thức, chứng minh và cách vẽ đường trung tuyến ngay sau đây!
Đường trung tuyến là gì?
Đường trung tuyến là một khái niệm trong hình học, nó là một đoạn thẳng đi qua trung điểm của một đoạn thẳng hay nối từ đỉnh của một tam giác đến trung điểm của cạnh đối diện.
Định nghĩa đường trung tuyến của đoạn thẳng:
- Đường trung tuyến của đoạn thẳng là một đường thẳng đi qua trung điểm của đoạn thẳng đó. Nó chia đoạn thẳng ban đầu thành hai đoạn có chiều dài bằng nhau.
Định nghĩa đường trung tuyến của tam giác:
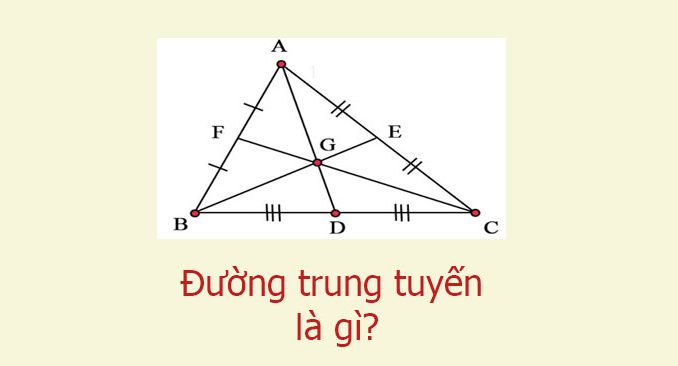
- Đường trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác đều có ba đường trung tuyến.
Ví dụ về đường trung tuyến của tam giác
Xét tam giác ABC có đỉnh A, đỉnh B, đỉnh C và cạnh AB, cạnh AC, cạnh BC. Đường trung tuyến của tam giác ABC là ba đoạn thẳng AM, BN, CN.
Trong đó:
- AM là đường trung tuyến ứng với cạnh BC.
- BN là đường trung tuyến ứng với cạnh AC.
- CN là đường trung tuyến ứng với cạnh AB.
- Ứng dụng của đường trung tuyến trong tam giác
Đường trung tuyến của tam giác có nhiều ứng dụng trong thực tế và trong toán học, chẳng hạn như:
- Dùng để tính diện tích tam giác.
- Dùng để tính độ cao của tam giác.
- Dùng để tính khoảng cách giữa hai điểm trong tam giác.
- Dùng để kiểm tra tính cân bằng của tam giác.
>>> Tìm hiểu thêm: Các dạng bài tập toán lớp 6 về số nguyên
Giao 3 đường truy tuyến là gì?
Giao 3 đường truy tuyến là giao điểm của 3 đường truy tuyến của một tam giác. Đường truy tuyến của một tam giác là đường thẳng đi qua đỉnh của tam giác và tiếp xúc với một cạnh đối diện. Trong một tam giác bất kỳ, ta có 3 đường truy tuyến. Ba đường truy tuyến này cùng đi qua một điểm, gọi là trọng tâm của tam giác.
- Vậy, giao 3 đường truy tuyến của một tam giác là trọng tâm của tam giác đó.
Tính chất của giao 3 đường truy tuyến:
- Giao 3 đường truy tuyến của một tam giác là trọng tâm của tam giác đó.
- Khoảng cách từ trọng tâm đến mỗi đỉnh bằng 2/3 độ dài đường truy tuyến đi qua đỉnh đó.
- Giao 3 đường truy tuyến chia tam giác thành 6 tam giác nhỏ có diện tích bằng nhau.
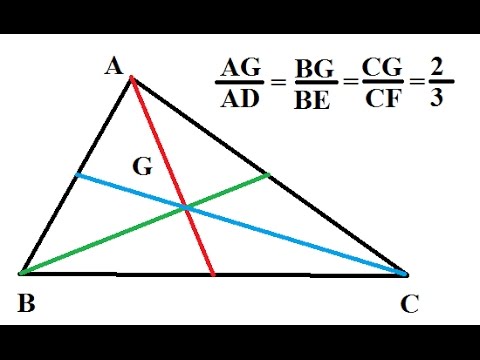
Ví dụ:
Cho tam giác ABC với các đường truy tuyến AD, BE, CF. Giao điểm của 3 đường truy tuyến này là G.
Ta có:
- G là trọng tâm của tam giác ABC.
- GA = 2/3 AD, GB = 2/3 BE, GC = 2/3 CF.
- AG/AC = BG/BC = CG/AB = 2/3.
Tam giác ABG, BCG, CGA là các tam giác nhỏ có diện tích bằng nhau.
Diện tích tam giác ABC = 3 * diện tích tam giác ABG.
Tính chất đường trung tuyến là gì?
Đường trung tuyến của tam giác là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Mỗi tam giác có ba đường trung tuyến.
Tính chất đường trung tuyến của tam giác bao gồm:
- Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó được gọi là trọng tâm của tam giác.
- Khoảng cách từ trọng tâm đến đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
- Mỗi đường trung tuyến chia tam giác thành hai tam giác có diện tích bằng nhau.
- Ba đường trung tuyến chia tam giác thành sáu tam giác nhỏ có diện tích bằng nhau.
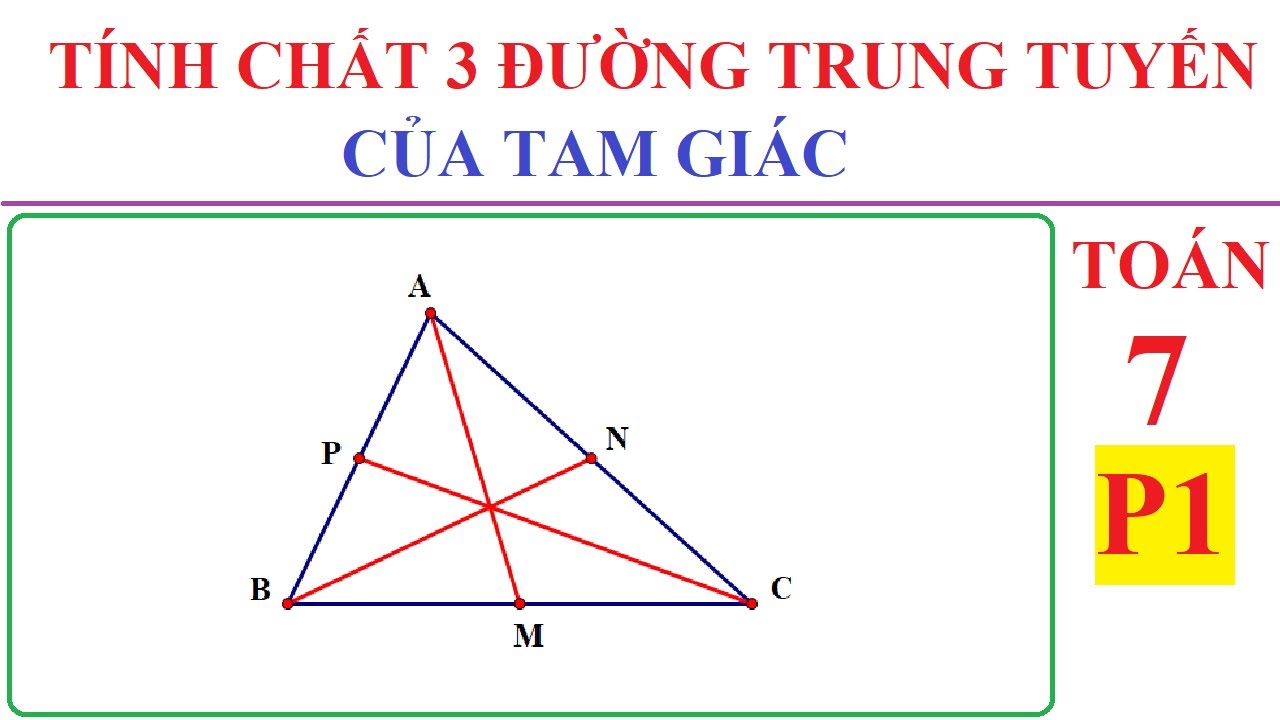
Tính chất đường trung tuyến trong tam giác cân và tam giác đều:
- Trong tam giác cân, đường trung tuyến ứng với cạnh đáy chia tam giác thành hai tam giác bằng nhau.
- Trong tam giác đều, ba đường trung tuyến đồng qui tại tâm của đường tròn nội tiếp tam giác.
>>> Xem thêm: 100 Đề Bài tập Toán lớp 1 nâng cao khó cho học sinh giỏi có lời giải
Tính chất đường trung tuyến trong tam giác vuông
Đường trung tuyến của tam giác vuông là đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền sẽ có độ dài bằng 1/2 cạnh huyền.
Đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền.
Đây là tính chất đặc trưng của đường trung tuyến trong tam giác vuông. Tính chất này có thể được chứng minh bằng cách chia tam giác vuông thành hai tam giác nhỏ bằng nhau.
Một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
Tính chất này cũng có thể được chứng minh bằng cách sử dụng tính chất đường trung tuyến trong tam giác vuông.
Ví dụ
Cho tam giác vuông ABC với AB là cạnh huyền. Đường trung tuyến AM ứng với cạnh huyền AB có độ dài bằng 12 cm. Tính BC.
Áp dụng tính chất đường trung tuyến trong tam giác vuông, ta có:
- AM = 1/2 AB
- 12 = 1/2 AB
- AB = 12 * 2 = 24 cm
- Vậy BC = 24 cm.
Tính chất đường trung tuyến trong tam giác cân
Trong tam giác cân, đường trung tuyến ứng với cạnh đáy là đoạn thẳng vuông góc với cạnh đáy và chia tam giác thành hai tam giác nhỏ bằng nhau.
Giả sử tam giác ABC cân tại đỉnh A. Đường trung tuyến AM ứng với cạnh đáy BC.
AM vuông góc với BC:
Từ đỉnh A, kẻ hai đường vuông góc với BC tại M và N.
Do tam giác ABC cân tại đỉnh A nên AB = AC => AN = BC/2
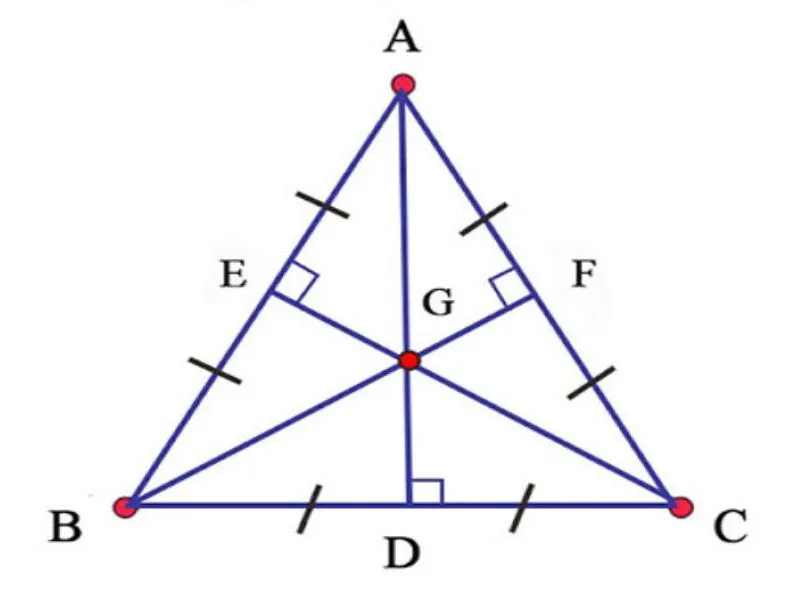
Do M là trung điểm của BC nên BM = CN = BC/2
=> AM = MN = BC/2
=> AM vuông góc với BC (theo định lý Pythagoras)
AM chia tam giác ABC thành hai tam giác bằng nhau:
- Do AM vuông góc với BC nên tam giác ABM và tam giác ACM là hai tam giác vuông cân.
- Do BM = CM = BC/2 nên tam giác ABM và tam giác ACM có cùng diện tích.
=> Tam giác ABC được chia thành hai tam giác bằng nhau.
Kết luận: Trong tam giác cân, đường trung tuyến ứng với cạnh đáy là đoạn thẳng vuông góc với cạnh đáy và chia tam giác thành hai tam giác nhỏ bằng nhau.
>>> Tìm hiểu thêm: Các dạng bài tập Toán lớp 6 học kì 2
Công thức tính đường trung tuyến của tam giác
Đối với tam giác vuông:
- Đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền.
- Đường trung tuyến ứng với cạnh góc vuông bằng ½√(cạnh góc vuông)^2 – (cạnh huyền – cạnh góc vuông)^2.
Đối với tam giác bất kỳ:
Đường trung tuyến ứng với cạnh a bằng:
- √(b^2 – (a – c)^2)/2
- √(c^2 – (a – b)^2)/2
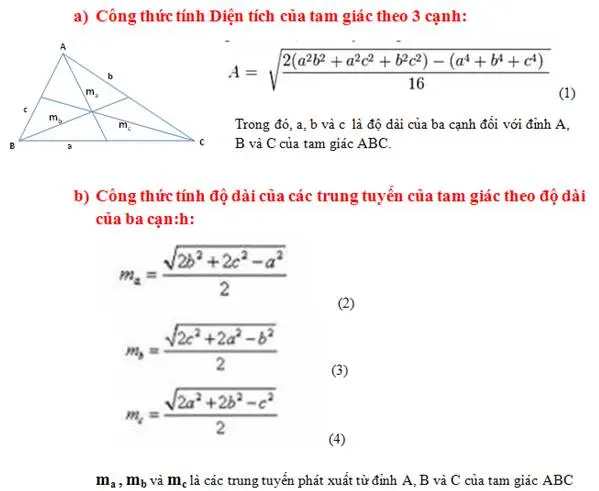
Đường trung tuyến ứng với cạnh b bằng:
- √(a^2 – (b – c)^2)/2
- √(c^2 – (b – a)^2)/2
Đường trung tuyến ứng với cạnh c bằng:
- √(a^2 – (c – b)^2)/2
- √(b^2 – (c – a)^2)/2
Tính chất đường trung tuyến của tam giác có nhiều ứng dụng trong thực tế, đặc biệt là trong các bài toán hình học.
Công thức tính độ dài của đường trung tuyến
Công thức tính độ dài của đường trung tuyến của tam giác là:
d = s * r
Trong đó:
- d là độ dài của đường trung tuyến
- s là nửa chu vi tam giác
- r là bán kính đường tròn ngoại tiếp tam giác
Để tính độ dài của đường trung tuyến, ta có thể thực hiện theo các bước sau:
Tính nửa chu vi tam giác:
s = (a + b + c) / 2
Trong đó:
- a, b, c là các cạnh của tam giác
Tính bán kính đường tròn ngoại tiếp tam giác:
- r = s * R / s
Trong đó:
R là bán kính đường tròn nội tiếp tam giác
- Thay các giá trị đã tính được vào công thức ban đầu để tính độ dài của đường trung tuyến:
- d = s * r
Ví dụ:
Cho tam giác ABC với các cạnh a = 3 cm, b = 4 cm, c = 5 cm. Tính độ dài của đường trung tuyến AM.
Ta có:
- s = (3 + 4 + 5) / 2 = 6
- R = (s * r) / s = (6 * 5) / 6 = 5
- d = s * r = 6 * 5 = 30
Vậy độ dài của đường trung tuyến AM là 30 cm.
>>> Tìm hiểu thêm: Các dạng toán vi-ét thi vào lớp 10 có đáp án chuẩn nhất
Công thức đường trung tuyến trong tam giác đều cạnh a
Trong tam giác đều, các cạnh đều bằng nhau nên đường trung tuyến cũng bằng nhau. Công thức đường trung tuyến trong tam giác đều cạnh a là:
d = a/2
Trong đó:
- d là độ dài đường trung tuyến
- a là độ dài cạnh của tam giác đều
Ví dụ: Tam giác đều ABC có cạnh a = 10 cm. Đường trung tuyến AM có độ dài là:
AM = a/2 = 10/2 = 5 cm
Ngoài ra, ba đường trung tuyến trong tam giác đều cắt nhau tại trọng tâm tam giác, và mỗi đường trung tuyến chia tam giác thành hai tam giác có diện tích bằng nhau.
Cách chứng minh đường trung tuyến
Đường trung tuyến của một tam giác là đoạn thẳng nối từ một đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác đều có ba trung tuyến. Để chứng minh tính chất của đường trung tuyến, ta thường sử dụng các bước sau:
- Vẽ hình và xác định các yếu tố cần thiết.
- Sử dụng các định lý, tính chất đã biết để chứng minh.
- Rút ra kết luận.
Ví dụ
Chứng minh đường trung tuyến của tam giác vuông ứng với cạnh huyền bằng 1/2 cạnh huyền.
Bước 1: Vẽ hình và xác định các yếu tố cần thiết.
- Cho tam giác ABC vuông tại A, với AB là cạnh huyền.
- Tam giác ABC vuông tại A
Bước 2: Sử dụng các định lý, tính chất đã biết để chứng minh.
Ta có:
- ΔABC ~ ΔABM (cạnh huyền tương ứng bằng nhau)
- BM = MC (định nghĩa trung điểm)
Kết luận:
- AB/AM = BM/MC
- AB/2 = BM/MC
- AB/2 = 1/2 (BM + MC)
- AB/2 = 1/2 * BC
- AB = 1/2 * BC
Bước 3: Rút ra kết luận.
- Vậy, đường trung tuyến của tam giác vuông ứng với cạnh huyền bằng 1/2 cạnh huyền.
Cách vẽ đường trung tuyến
Đường trung tuyến là đường thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Mỗi tam giác đều có ba trung tuyến.
Để vẽ đường trung tuyến của một tam giác, ta thực hiện theo các bước sau:
- Vẽ tam giác trên giấy hoặc trên màn hình máy tính.
- Xác định đỉnh và trung điểm của cạnh đối diện.
- Dùng thước kẻ hoặc công cụ vẽ để nối đỉnh và trung điểm.
- Cách xác định trung điểm của cạnh
Để xác định trung điểm của cạnh, ta thực hiện theo các bước sau:
- Vẽ đường trung trực của cạnh.
- Điểm giao giữa đường trung trực và cạnh chính là trung điểm của cạnh.
Ví dụ
Trên hình vẽ bên, ta có tam giác ABC. Để vẽ đường trung tuyến AM, ta thực hiện các bước sau:
- Vẽ tam giác ABC trên giấy.
- Xác định đỉnh A và trung điểm M của cạnh BC.
- Dùng thước kẻ để nối đỉnh A và trung điểm M.
- Kết quả ta được đường trung tuyến AM.
- Tính chất của đường trung tuyến
Đường trung tuyến của tam giác có các tính chất sau:
- Đi qua trung điểm của cạnh đối diện.
- Chia tam giác thành hai tam giác có diện tích bằng nhau.
- Ba trung tuyến của tam giác cắt nhau tại một điểm gọi là trọng tâm của tam giác.
Bài tập về đường trung tuyến
Bài tập về đường trung tuyến của tam giác thường được chia thành các dạng sau:
Dạng 1: Tính chất ba đường trung tuyến của tam giác.
Dạng bài tập này thường yêu cầu học sinh chứng minh các tính chất của ba đường trung tuyến của tam giác, như:
* Ba đường trung tuyến của tam giác cùng đi qua một điểm.
* Điểm đó cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.
* Ba đường trung tuyến chia tam giác thành 9 tam giác nhỏ bằng nhau.
Dạng 2: Tính độ dài đường trung tuyến của tam giác.
Dạng bài tập này thường yêu cầu học sinh tính độ dài đường trung tuyến của tam giác khi biết các cạnh của tam giác hoặc các độ dài của các cạnh của tam giác.
Dạng 3: Tính các yếu tố của tam giác khi biết đường trung tuyến của tam giác.
Dạng bài tập này thường yêu cầu học sinh tính các yếu tố của tam giác như: cạnh, góc, diện tích,… khi biết đường trung tuyến của tam giác.
Dưới đây là một số ví dụ về bài tập về đường trung tuyến của tam giác và lời giải:
Ví dụ 1
Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Tính độ dài đường trung tuyến AD.
Lời giải:
Áp dụng định lý Pythagore vào tam giác ABC ta có:
- AC^2 = AB^2 + BC^2
- 8^2 = 6^2 + 10^2
- AC = 10
Độ dài đường trung tuyến AD bằng:
- AD = AC/2 = 10/2 = 5 cm
Ví dụ 2
Cho tam giác ABC có đường trung tuyến AD = 6 cm. Tính độ dài cạnh BC.
Lời giải:
Gọi E là trung điểm của cạnh BC. Khi đó, đường trung tuyến AD là phân giác của góc BAC.
- AD/BC = AB/AC
- 6/BC = 6/8
- BC = 8/6 * 6 = 8 cm
Ví dụ 3
Cho tam giác ABC có trọng tâm G. Biết GA = 2 cm và GB = 3 cm. Tính độ dài cạnh BC.
Lời giải:
Ta có:
- GA + GB = GC
- 2 + 3 = GC
- GC = 5 cm
Độ dài cạnh BC bằng:
- BC = 2GC = 2 * 5 = 10 cm
Ví dụ 4
Cho tam giác ABC có đường trung tuyến AD. Trên tia đối của tia DA lấy điểm M sao cho DM = 1/3 AD. Tính khoảng cách từ M đến cạnh BC.
Lời giải:
Ta có:
- DM/AD = 1/3
- DM = AD/3
- DM = 6/3 = 2 cm
Khoảng cách từ M đến cạnh BC bằng:
- BM + MC = BC
- BM + MC = 10
- BM + 2 = 10
- BM = 10 – 2 = 8 cm
Vậy, khoảng cách từ M đến cạnh BC là 8 cm.
Trên đây là một số dạng bài tập về đường trung tuyến của tam giác và lời giải. Để giải tốt các bài tập này, học sinh cần nắm vững lý thuyết về đường trung tuyến của tam giác.
Qua bài viết trên, hy vọng mọi người đã rõ hơn về thắc mắc đường trung tuyến là gì? Mong rằng bài viết trên đã cung cấp cho bạn những kiến thức hữu ích về đường trung tuyến của tam giác. Ngoài ra, bạn cũng có thể tham khảo thêm một số bài tập về đường trung tuyến của tam giác để củng cố kiến thức của mình.